
| A. | 4 | B. | 2 | C. | 1 | D. | 0 |
分析 由已知数列递推式求得a5、a6的值,再结合偶函数f(x)满足f(x)=f(x+2),f(-1)=1求得f(a5)+f(a6).
解答 解:由2Sn=an+1,得2Sn-1=an(n≥2),
∴2an=an+1-an,得an+1=3an(n≥2),
又由2Sn=an+1,a1=$\frac{1}{2}$,得a2=1.
∴${a}_{5}=1×{3}^{3}=27$,${a}_{6}=1×{3}^{4}=81$.
由偶函数f(x)满足f(x)=f(x+2),可得函数f(x)的周期为2,
∴f(a5)=f(27)=f(-1)=1;
f(a6)=f(81)=f(1)=f(-1)=1,
∴f(a5)+f(a6)=1+1=2.
故选:B.
点评 本题考查数列递推式,考查了数列的函数特性,训练了函数周期性与奇偶性的应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “m=-2”是“直线mx+(m-1)y-1=0与直线3x+my+2=0垂直”的充分不必要条件 | |
| B. | 已知a∈R,则“a<1”是“|x-2|+|x|>a”恒成立的必要不充分条件 | |
| C. | 设p,q是两个命题,若¬(p∧q)是假命题,则p,q均为真命题 | |
| D. | 命题p:“?x∈R,使得x2+x+1<0”,则¬p:“?x∈R,均有x2+x+1≥0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
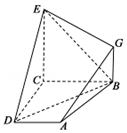 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2,AD=BG=1.
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2,AD=BG=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(π)>f(-2)>f(-1) | B. | f(π)>f(-1)>f(-2) | C. | f(π)<f(-2)<f(-1) | D. | f(π)<f(-1)<f(-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{2}$-1 | C. | $\sqrt{2}$-1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com