
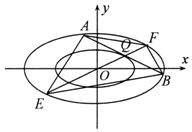
 在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.
在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.分析 (Ⅰ)由椭圆的离心率为$\frac{{\sqrt{2}}}{2}$、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8,列出方程,求出a,b,由此能求出椭圆C1的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$.
(Ⅱ)(i)由(Ⅰ)知椭圆C2:$\frac{{x}^{2}}{2}+{y}^{2}$=1,Q(x0,y0)为椭圆E上一点,$\frac{{{x}_{0}}^{2}}{2}+{{y}_{0}}^{2}$=1,利用点差法求出直线AB的方程为x0x+2y0y=2,由此能求出直线AB的方程.
(Ⅲ)联立直线EF与椭圆C1的方程$\left\{\begin{array}{l}{{y}_{0}x-{x}_{0}y=0}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,得E($\sqrt{2}{x}_{0}$,$\sqrt{2}{y}_{0}$),F(-$\sqrt{2}{x}_{0}$,-$\sqrt{2}{y}_{0}$),联立直线AB与椭圆C1的方程$\left\{\begin{array}{l}{{x}_{0}x+2{y}_{0}y=2}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,得:$2{x}^{2}-4{x}_{0}x+4-8{{y}_{0}}^{2}=0$,利用韦达定理求出|AB|=$\sqrt{8{{y}_{0}}^{2}+2{{x}_{0}}^{2}}$,点E($\sqrt{2}{x}_{0},\sqrt{2}{y}_{0}$)、F(-$\sqrt{2}{x}_{0},-\sqrt{2}{y}_{0}$)到直线AB的距离为d1,d2,--由此能求出当Q在椭圆C2上移动时,四边形AEBF的面积为定值4.
解答 解:(Ⅰ)∵椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,
左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.
∴e=$\frac{c}{a}=\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{2}}{2}$,∴a2=2b2,
∵P是椭圆C1上任意一点,∴|PF1|+|PF2|=2a,
$\frac{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}}{2}$≥($\frac{|P{F}_{1}|+|P{F}_{2}|}{2}$)2=a2,
∴2a2=8,a2=4,b2=2,
∴椭圆C1的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1.
(Ⅱ)(i)证明:由(Ⅰ)知椭圆C2:$\frac{{x}^{2}}{2}+{y}^{2}$=1,Q(x0,y0)为椭圆E上一点,
$\frac{{{x}_{0}}^{2}}{2}+{{y}_{0}}^{2}$=1,
当y0≠0,设A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{2}=1,①}\\{\frac{{{x}_{2}}^{2}}{4}+\frac{{{y}_{2}}^{2}}{2}=1,②}\end{array}\right.$
②-①,整理,得:$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}=-\frac{{x}_{2}+{x}_{1}}{2({y}_{2}+{y}_{1})}$,
∵Q为线段AB的中点,∴$-\frac{{x}_{2}+{x}_{1}}{2({y}_{2}+{y}_{1})}$=-$\frac{2{x}_{0}}{4{y}_{0}}$=-$\frac{{x}_{0}}{2{y}_{0}}$,
∴直线AB的斜率为$-\frac{{x}_{0}}{2{y}_{0}}$,∴直线AB的方程为y-y0=-$\frac{{x}_{0}}{2{y}_{0}}$(x-x0),
∵$\frac{{{x}_{0}}^{2}}{2}+{{y}_{0}}^{2}$=1,化简,得x0x+2y0y=2,
当${y}_{0}=0,{x}_{0}=±\sqrt{2}$时,直线AB的方程也满足x0x+2y0y=2,
综上,直线AB的方程为x0x+2y0y=2.
(ii)直线EF的方程为y0x-x0y=0,
联立直线EF与椭圆C1的方程$\left\{\begin{array}{l}{{y}_{0}x-{x}_{0}y=0}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,
解得E($\sqrt{2}{x}_{0}$,$\sqrt{2}{y}_{0}$),F(-$\sqrt{2}{x}_{0}$,-$\sqrt{2}{y}_{0}$),
联立直线AB与椭圆C1的方程$\left\{\begin{array}{l}{{x}_{0}x+2{y}_{0}y=2}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,
消去y,得:$2{x}^{2}-4{x}_{0}x+4-8{{y}_{0}}^{2}=0$,
x1+x2=2x0,x1x2=2-4y02,
|AB|=$\sqrt{1+(-\frac{{{x}_{0}}^{2}}{2{y}_{0}})^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{\frac{4{{y}_{0}}^{2}+{{x}_{0}}^{2}}{4{{y}_{0}}^{2}}}$•$\sqrt{4{{x}_{0}}^{2}-8+16{{y}_{0}}^{2}}$=$\sqrt{8{{y}_{0}}^{2}+2{{x}_{0}}^{2}}$,
设点E($\sqrt{2}{x}_{0},\sqrt{2}{y}_{0}$)、F(-$\sqrt{2}{x}_{0},-\sqrt{2}{y}_{0}$)到直线AB的距离分别为d1,d2,
SAEBF=S△ABE+S△ABF=$\frac{1}{2}|AB|({d}_{1}+{d}_{2})$,
${d}_{1}=\frac{|-2\sqrt{2}{{y}_{0}}^{2}+\sqrt{2}{{{x}_{0}}^{2}-2}_{\;}|}{\sqrt{4{{y}_{0}}^{2}+{{x}_{0}}^{2}}}$=$\frac{|-\sqrt{2}(2{{y}_{0}}^{2}+{{x}_{0}}^{2})-2|}{\sqrt{4{{y}_{0}}^{2}+{{x}_{0}}^{2}}}$=$\frac{2\sqrt{2}-2}{\sqrt{4{{y}_{0}}^{2}+{{x}_{0}}^{2}}}$,
${d}_{2}=\frac{|-2\sqrt{2}{{y}_{0}}^{2}-\sqrt{2}{{x}_{0}}^{2}-2|}{\sqrt{4{{y}_{0}}^{2}+{{x}_{0}}^{2}}}$=$\frac{|-\sqrt{2}(2{{y}_{0}}^{2}+{{x}_{0}}^{2})-2|}{\sqrt{4{{y}_{0}}^{2}+{{x}_{0}}^{2}}}$=$\frac{2\sqrt{2}+2}{\sqrt{4{{y}_{0}}^{2}+{{x}_{0}}^{2}}}$,
∴SAEBF=$\frac{1}{2}|AB|({d}_{1}+{d}_{2})=\frac{1}{2}\sqrt{8{{y}_{0}}^{2}+2{{x}_{0}}^{2}}$•=$\frac{2\sqrt{2}-2+2\sqrt{2}+2}{\sqrt{4{{y}_{0}}^{2}+{{x}_{0}}^{2}}}$=4.
故当Q在椭圆C2上移动时,四边形AEBF的面积为定值4.
点评 本题考查椭圆方程、两线段和的取值范围、椭圆性质、直线方程等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | -$\frac{\sqrt{2}}{4}$ | C. | 2$\sqrt{2}$ | D. | -2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3<k<1 | B. | k>1 | C. | -1<k<1 | D. | -1<k<3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{π}{12}$ | B. | $x=\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.图1是源于其思想的一个程序框图,若输入的a,b分别为4,2,则输出的n等于( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.图1是源于其思想的一个程序框图,若输入的a,b分别为4,2,则输出的n等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com