
| A. | $x=\frac{π}{12}$ | B. | $x=\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=\frac{5π}{12}$ |
分析 利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,结合三角函数的图象和性质,可得对称轴方程.即可判断.
解答 解:函数$f(x)={sin^2}x+\sqrt{3}sinxcosx$,
化简可得:f(x)=$\frac{1}{2}$$-\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x=sin(2x-$\frac{π}{6}$)$+\frac{1}{2}$.
对称轴方程为:2x-$\frac{π}{6}$=$\frac{π}{2}+kπ$,k∈Z,
得:x=$\frac{1}{2}kπ+\frac{π}{3}$,k∈Z,
当k=0,可得一条对称轴为x=$\frac{π}{3}$.
故选C
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
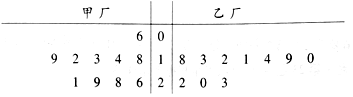 某种产品的产量以其质量指标值(单位:克)衡量,质量指标值越大表明质量越好,且质量指标值大于17时,该产品为优等品,现在为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取10件样品,测量样品的质量指标值,得到如图所示的茎叶图.
某种产品的产量以其质量指标值(单位:克)衡量,质量指标值越大表明质量越好,且质量指标值大于17时,该产品为优等品,现在为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取10件样品,测量样品的质量指标值,得到如图所示的茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
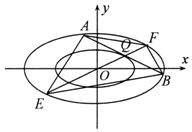 在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.
在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 内心 | B. | 外心 | C. | 重心 | D. | 垂心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在等腰三角形ABC中,已知|AB|=|AC|=1,∠A=120°,E,F分别是AB,AC上的点,且$\overrightarrow{AE}=λ\overrightarrow{AB},\overrightarrow{AF}=μ\overrightarrow{AC}$,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则$\overrightarrow{MN}$的最小值为$\frac{\sqrt{7}}{7}$.
如图,在等腰三角形ABC中,已知|AB|=|AC|=1,∠A=120°,E,F分别是AB,AC上的点,且$\overrightarrow{AE}=λ\overrightarrow{AB},\overrightarrow{AF}=μ\overrightarrow{AC}$,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则$\overrightarrow{MN}$的最小值为$\frac{\sqrt{7}}{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com