练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．图1是源于其思想的一个程序框图，若输入的a，b分别为4，2，则输出的n等于（　　）
    A．2B．3C．4D．5

    分析 模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．

    解答 解：模拟程序的运行，可得
    a=4，b=2，n=1，
    a=6，b=4，
    不满足循环的条件a≤b，执行循环体，n=2，a=9，b=8
    不满足循环的条件a≤b，执行循环体，n=3，a=13.5，b=16
    满足循环的条件a≤b，退出循环，输出n的值为3．
    故选：B．

    点评 本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．在△ABC中，命题p：“B≠60°“，命题q：“△ABC的三个内角A，B，C不成等差数列“，那么p是q的
    （　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

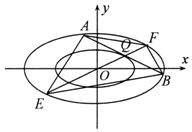    18．在直角坐标系xOy中，椭圆C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，左、右焦点分别是F1，F2，P为椭圆C1上任意一点，|PF1|2+|PF2|2的最小值为8．
    （I）求椭圆C1的方程；
    （II）设椭圆C2：$\frac{{2{x^2}}}{a^2}+\frac{{2{y^2}}}{b^2}=1，Q（{{x_0}，{y_0}}）$为椭圆C2上一点，过点Q的直线交椭圆C1于A，B两点，且Q为线段AB的中点，过O，Q两点的直线交椭圆C1于E，F两点．
    （i）求证：直线AB的方程为x0x+2y0y=2；
    （ii）当Q在椭圆C2上移动时，四边形AEBF的面积是否为定值？若是，求出该定值；不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．执行如图所示程序框图，若输入的k=4，则输出的s=（　　）
    A．$\frac{1}{3}$B．$\frac{4}{5}$C．$\frac{5}{6}$D．$\frac{6}{7}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．对于函数f（x）给出定义：设f′（x）是函数f（x）的导函数，f″（x）是函数f′（x）的导函数，若函数f″（x）有零点x0，则称（x0，f（x0））为函数f（x）的“拐点”．某同学经过探究发现：任何一个三次函数f（x）=ax3+bx2+cx+d（a≠0）都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心，给定函数f（x）=$\frac{1}{3}$x3-x2-$\frac{1}{3}$x+2，请你根据上面探究结果，计算$\sum_{i1}^{4035}$f（$\frac{i}{2017}$）=4035．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知椭圆C：$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，点$P（\sqrt{2}，2）$在椭圆上．
    （1）求椭圆C的方程；
    （2）过椭圆上的焦点F作两条相互垂直的弦AC，BD，求|AC|+|BD|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设点O、P、Q是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线与抛物线y2=4x的交点，O为坐标原点，若△OPQ的面积为2，则双曲线的离心率为$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．设Sn为等差数列{an}的前n项和，且a3=5，S6=42，则S9=117．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=3，|$\overrightarrow{a}$-$\overrightarrow{b}$|=1，$\overrightarrow{a}$与$\overrightarrow{b}$夹角为θ，则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|cosθ}$+$\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|cosθ}$=（　　）
    A．$\frac{1}{2}$B．$\frac{5}{2}$C．$\frac{5}{4}$D．3

    查看答案和解析>>

    同步练习册答案