
分析 直接利用定义判断①;利用反例判断②;利用定义推出m的范围判断③;利用分析法直接证明结合函数的导数判断④.
解答 解:①∵$\frac{f(π)-f(-π)}{2π}$=0,而f($\frac{π}{2}$)=0,
∴f(x)=sinx-1是[-π,π]上的“平均值函数”,故①正确;
②若f(x)=0,则$\frac{f(b)-f(a)}{b-a}$=0,显然(a,b)上的任意1个数都是f(x)的均值点,故②错误;
③若函数f(x)=x2+mx-1是[-1,1]上的“平均值函数”,
则区间(-1,1)上存在x0使得f(x0)=$\frac{f(1)-f(-1)}{2}$=m,
即x02+mx0-1=m,∴m=$\frac{{{x}_{0}}^{2}-1}{1-{x}_{0}}$=-x0-1,
∵x0∈(-1,1),∴m∈(-2,0).故③正确;
④若f(x)=lnx是区间[a,b](b>a≥1)上的“平均值函数”,x0是它的一个均值点,
∴lnx0=$\frac{lnb-lna}{b-a}$=$\frac{ln\frac{b}{a}}{b-a}$,则lnx0-$\frac{1}{{\sqrt{ab}}}$=$\frac{ln\frac{b}{a}}{b-a}$-$\frac{1}{{\sqrt{ab}}}$.
令$\sqrt{\frac{b}{a}}$=t,则b=at2(t>1),
∴$\frac{ln\frac{b}{a}}{b-a}$-$\frac{1}{{\sqrt{ab}}}$=$\frac{ln{t}^{2}}{a({t}^{2}-1)}$-$\frac{1}{at}$=$\frac{1}{a}$($\frac{ln{t}^{2}}{{t}^{2}-1}-\frac{1}{t}$)=$\frac{1}{a{t}^{2}({t}^{2}-1)}$(2lnt-t+$\frac{1}{t}$),
令g(t)=2lnt-t+$\frac{1}{t}$,则g′(t)=$\frac{2}{t}-1-\frac{1}{{t}^{2}}$=$\frac{2t-{t}^{2}-1}{{t}^{2}}$=$\frac{-(t-1)^{2}}{{t}^{2}}$<0,
∴g(t)在(1,+∞)上是减函数,
∴g(t)<g(1)=0,
∴$\frac{ln\frac{b}{a}}{b-a}$-$\frac{1}{{\sqrt{ab}}}$<0,即lnx0<$\frac{1}{\sqrt{ab}}$,故④正确.
故答案为:①③④.
点评 本题考查新定义的应用,函数的导数以及分析法的应用,考查分析问题解决问题的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{5}+\frac{1}{5}i$ | B. | $\frac{2}{5}-\frac{1}{5}i$ | C. | $\frac{2}{5}+\frac{1}{5}i$ | D. | $-\frac{2}{5}-\frac{1}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | -1+2i | C. | 1-2i | D. | -1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | a2<ab | C. | a2<b2 | D. | $\frac{1}{a-b}<\frac{1}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
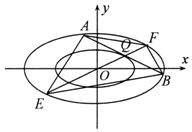 在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.
在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|2+|PF2|2的最小值为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com