
分析 (I)曲线C的参数方程为$\left\{{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}({θ为参数})}\right.$,利用平方关系即可化为普通方程.利用变换公式代入即可得出曲线C'的直角坐标方程,利用互化公式可得极坐标方程.
(II)点$A(\frac{3}{2},π)$直角坐标是$A(-\frac{3}{2},0)$,将l的参数方程$\left\{{\begin{array}{l}{x=-2+tcos\frac{π}{6}}\\{y=tsin\frac{π}{6}}\end{array}}\right.$代入曲线C'的直角坐标方程可得$4{t^2}-6\sqrt{3}t+5=0$,利用根与系数的关系即可得出.
解答 解:(Ⅰ)$C:\left\{{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}}\right.⇒C:\frac{x^2}{4}+\frac{y^2}{3}=1$,(2分)
将$\left\{{\begin{array}{l}{x'=\frac{1}{2}x}\\{y'=\frac{1}{{\sqrt{3}}}y}\end{array}}\right.⇒\left\{{\begin{array}{l}{x=2x'}\\{y=\sqrt{3}y'}\end{array}}\right.$,代入C的普通方程可得x'2+y'2=1,(4分)
即C':x2+y2=1,所以曲线C'的极坐标方程为 C':ρ=1(5分)
(Ⅱ)点$A(\frac{3}{2},π)$直角坐标是$A(-\frac{3}{2},0)$,将l的参数方程$\left\{{\begin{array}{l}{x=-2+tcos\frac{π}{6}}\\{y=tsin\frac{π}{6}}\end{array}}\right.$
代入x2+y2=1,可得$4{t^2}-6\sqrt{3}t+5=0$,(8分)
∴t1+t2=$\frac{3\sqrt{3}}{2}$,t1•t2=$\frac{5}{4}$,
所以$\frac{|AP|}{|AM|•|AN|}=\frac{{|\frac{{{t_1}+{t_2}}}{2}|}}{{|{t_1}{t_2}|}}=\frac{{3\sqrt{3}}}{5}$. (10分)
点评 本题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:解答题
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 10 | ||
| 女生 | 20 | ||
| 合计 |
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
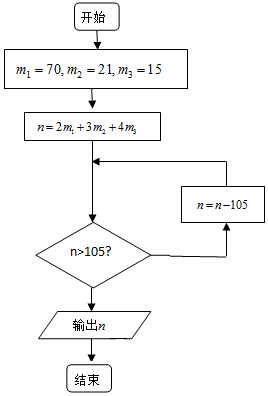 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子口诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此口诀的算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子口诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此口诀的算法如图,则输出n的结果为( )| A. | 53 | B. | 54 | C. | 158 | D. | 263 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln2+$\frac{5}{8}$ | B. | ln2-$\frac{1}{2}$ | C. | ln2+$\frac{1}{8}$ | D. | ln2-$\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com