
| A. | ln2+$\frac{5}{8}$ | B. | ln2-$\frac{1}{2}$ | C. | ln2+$\frac{1}{8}$ | D. | ln2-$\frac{3}{8}$ |
分析 由约束条件作出可行域,再由题意求得a值,然后利用定积分求面积.
解答 解:由约束条件$\left\{\begin{array}{l}{x-y≥0}\\{y-\frac{1}{x}≤0}\\{y≥a,(0<a<1)}\end{array}\right.$作出可行域如图,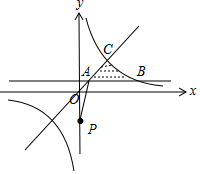
A(a,a),
z=$\frac{y+1}{x}$的最大值为P(0,-1)与A连线的斜率,等于${k}_{PA}=\frac{a+1}{a}=3$,则a=$\frac{1}{2}$.
∴区域D的面积为${∫}_{\frac{1}{2}}^{1}(x-\frac{1}{2})dx{+∫}_{1}^{2}(\frac{1}{x}-\frac{1}{2})dx$
=$(\frac{1}{2}{x}^{2}-\frac{1}{2}x){|}_{\frac{1}{2}}^{1}+(lnx-\frac{1}{2}x){|}_{1}^{2}$=$-\frac{1}{8}+\frac{1}{4}+ln2-1-ln1+\frac{1}{2}=ln2-$$\frac{3}{8}$.
故选:D.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,训练了利用定积分求曲边梯形的面积,是中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | x±y=0 | B. | $x±\sqrt{3}y=0$ | C. | $\sqrt{3}x±y=0$ | D. | 2x±y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x<-2”是“x2+3x+2>0”的必要不充分条件 | |
| B. | 对于命题p:?x0∈R,使得${x_0}^2+{x_0}-1<0$,则¬p:?x∈R,均有x2+x-1≥0 | |
| C. | 命题“若x2-3x+2=0,则x=2”的否命题为若x2-3x+2=0,则x≠2 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{5}+\frac{1}{5}i$ | B. | $\frac{2}{5}-\frac{1}{5}i$ | C. | $\frac{2}{5}+\frac{1}{5}i$ | D. | $-\frac{2}{5}-\frac{1}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | -1+2i | C. | 1-2i | D. | -1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
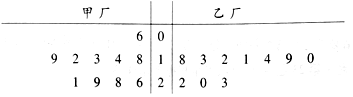 某种产品的产量以其质量指标值(单位:克)衡量,质量指标值越大表明质量越好,且质量指标值大于17时,该产品为优等品,现在为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取10件样品,测量样品的质量指标值,得到如图所示的茎叶图.
某种产品的产量以其质量指标值(单位:克)衡量,质量指标值越大表明质量越好,且质量指标值大于17时,该产品为优等品,现在为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取10件样品,测量样品的质量指标值,得到如图所示的茎叶图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com