
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{8}$ |
分析 根据已知条件,求出满足条件的正方形ABCD的面积,及该点到正方形的四条边的距离都大于1对应平面区域的面积,代入几何概型计算公式,即可求出答案.
解答 解:由题意,正方形的面积为4×4=16,
在边长为4的正方形内随机取一点,该点到正方形的四条边的距离都大于1,面积为2×2=4
由几何概型的公式,边长为4的正方形内随机取一点,该点到正方形的四条边的距离都大于1的概率是$\frac{4}{16}$=$\frac{1}{4}$,
故选:B.
点评 本题考查了几何概型的运用;几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据公式求值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知两灯塔A,D相距20海里,甲、乙两船同时从灯塔A处出发,分别沿与AD所成角相等的两条航线AB,AC航行,经过一段时间分别到达B,C两处,此时恰好B,D,C三点共线,且∠ABD=$\frac{π}{3}$,∠ADC=$\frac{7π}{12}$,则乙船航行的距离AC为( )
如图,已知两灯塔A,D相距20海里,甲、乙两船同时从灯塔A处出发,分别沿与AD所成角相等的两条航线AB,AC航行,经过一段时间分别到达B,C两处,此时恰好B,D,C三点共线,且∠ABD=$\frac{π}{3}$,∠ADC=$\frac{7π}{12}$,则乙船航行的距离AC为( )| A. | 10$\sqrt{6}$+10$\sqrt{2}$海里 | B. | 10$\sqrt{6}$-10$\sqrt{2}$海里 | C. | 40海里 | D. | 10$\sqrt{6}$+10$\sqrt{3}$海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
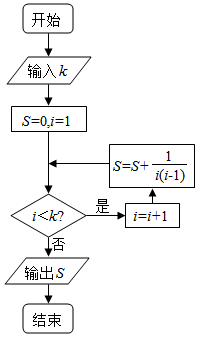
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
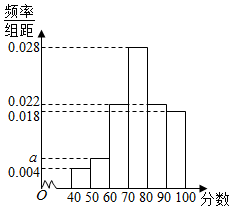 如图是根据某班50名同学在某次数学测验中的成绩(百分制)绘制的概率分布直方图,其中成绩分组区间为:[40,50),[50,60),…,[80,90),[90,100].
如图是根据某班50名同学在某次数学测验中的成绩(百分制)绘制的概率分布直方图,其中成绩分组区间为:[40,50),[50,60),…,[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com