
 某程序框图如图所示,若运行该程序后输出S为$\frac{5}{6}$.
某程序框图如图所示,若运行该程序后输出S为$\frac{5}{6}$. 分析 由图知,每次进入循环体后,S的值被累加运算,
由此运算规律进行计算,经过5次运算后输出结果即可.
解答 解:由图知运算规则是对S=S+$\frac{1}{{n}^{2}+n}$,故
第一次进入循环体后S=0+$\frac{1}{2}$=$\frac{1}{2}$,n=2
第二次进入循环体后S=$\frac{1}{2}$+$\frac{1}{6}$=$\frac{2}{3}$,n=3
第三次进入循环体后S=$\frac{2}{3}$+$\frac{1}{12}$=$\frac{3}{4}$,n=4
第四次进入循环体后S=$\frac{3}{4}$+$\frac{1}{20}$=$\frac{4}{5}$,n=5
第五次进入循环体后S=$\frac{4}{5}$+$\frac{1}{30}$=$\frac{5}{6}$,n=6
不满足循环条件,退出循环,输出s=$\frac{5}{6}$.
故答案为:$\frac{5}{6}$.
点评 本题考查了利用循环结构球累加运算的应用问题,是算法中一种常见的题型.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
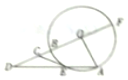 如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.
如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
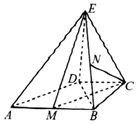 如图,在直角梯形ABCD中,AB∥CD,AB=2CD,∠BCD=90.,BC=CD,AE=BE,ED⊥平面ABCD.
如图,在直角梯形ABCD中,AB∥CD,AB=2CD,∠BCD=90.,BC=CD,AE=BE,ED⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
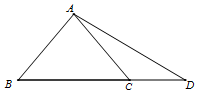 如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.
如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com