
【题目】在直角坐标系xoy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2
(t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2 ![]() cosθ. (Ⅰ)求C2与C3交点的直角坐标;
cosθ. (Ⅰ)求C2与C3交点的直角坐标;
(Ⅱ)若C2与C1相交于点A,C3与C1相交于点B,求|AB|的最大值.
【答案】解:(Ⅰ)曲线C2:ρ=2sinθ得ρ2=2ρsinθ,即x2+y2=2y,① C3:ρ=2 ![]() cosθ,则ρ2=2
cosθ,则ρ2=2 ![]() ρcosθ,即x2+y2=2
ρcosθ,即x2+y2=2 ![]() x,②
x,②
由①②得 ![]() 或
或 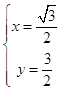 ,
,
即C2与C1交点的直角坐标为(0,0),( ![]() ,
, ![]() );
);
(Ⅱ)曲线C1的直角坐标方程为y=tanαx,
则极坐标方程为θ=α(ρ∈R,ρ≠0),其中0≤a<π.
因此A得到极坐标为(2sinα,α),B的极坐标为(2 ![]() cosα,α).
cosα,α).
所以|AB|=|2sinα﹣2 ![]() cosα|=4|sin(α-
cosα|=4|sin(α- ![]() )|,
)|,
当α= ![]() 时,|AB|取得最大值,最大值为4
时,|AB|取得最大值,最大值为4
【解析】(Ⅰ)将C2与C3转化为直角坐标方程,解方程组即可求出交点坐标;(Ⅱ)求出A,B的极坐标,利用距离公式进行求解.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,点![]() 坐标是
坐标是![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ;以极点为坐标原点,极轴为
;以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,斜率是
轴的正半轴建立平面直角坐标系,斜率是![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求证直线![]() 和曲线
和曲线![]() 相交于两点
相交于两点![]() 、
、![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
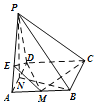
【题目】如图,四棱锥![]() 的底面ABCD是正方形,
的底面ABCD是正方形,![]() 为等边三角形,M,N分别是AB,AD的中点,且平面
为等边三角形,M,N分别是AB,AD的中点,且平面![]() 平面ABCD.
平面ABCD.
![]() 证明:
证明:![]() 平面PNB;
平面PNB;
![]() 设点E是棱PA上一点,若
设点E是棱PA上一点,若![]() 平面DEM,求
平面DEM,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点. 
(1)证明:EF∥BC;
(2)若AG等于⊙O的半径,且AE=MN=2 ![]() ,求四边形EBCF的面积.
,求四边形EBCF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)求![]() 的值;
的值;
(2)求函数![]() 的极小值;
的极小值;
(3)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数, 得到如下资料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取 2 组,用剩下的 4 组数据求 线性回归方程,再用被选取的 2 组数据进行检验;
(Ⅰ)求选取的 2 组数据恰好是相邻两个月的概率;
(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出 ![]() 关于
关于![]() 的线性回归方程 ;
的线性回归方程 ;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人, 则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
附:对于一组数据![]() ,
,![]() ,…,(
,…,(![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A套餐 | 50% | 25% | 25% |
B套餐 | 80% | 0 | 20% |
C套餐 | 50% | 50% | 0 |
D套餐 | 40% | 20% | 40% |
(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.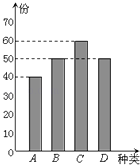
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDFE中,四边形ABCD是矩形,AB∥EF,AB=2EF,∠EAB=90°,平面ABFE⊥平面ABCD.

(1)若G点是DC的中点,求证:FG∥平面AED.
(2)求证:平面DAF⊥平面BAF.
(3)若AE=AD=1,AB=2,求三棱锥D-AFC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者![]() 和4名女志愿者
和4名女志愿者![]() ,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示。
,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示。
(1)求接受甲种心理暗示的志愿者中包含![]() 但不包含
但不包含![]() 的概率;
的概率;
(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com