练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．数列{an}前n项和为Sn，若${a_n}={2^{n-1}}$，则$C_n^1{S_1}+C_n^2{S_2}+…+C_n^n{S_n}$等于（　　）
    A．3n-2nB．2n-3nC．5n-2nD．3n-4n

    分析 利用等比数列的前n项和公式可得Sn=2n-1．再利用二项式定理即可得出．

    解答 解：Sn=$\frac{{2}^{n}-1}{2-1}$=2n-1．
    则$C_n^1{S_1}+C_n^2{S_2}+…+C_n^n{S_n}$=${∁}_{n}^{1}•2+{∁}_{n}^{2}•{2}^{2}$+…+${∁}_{n}^{n}•{2}^{n}$-$（{∁}_{n}^{1}+{∁}_{n}^{2}+…+{∁}_{n}^{n}）$=（2+1）n-1-[（1+1）n-1]=3n-2n．
    故选：A．

    点评 本题考查了等比数列的前n项和公式、二项式定理性质，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

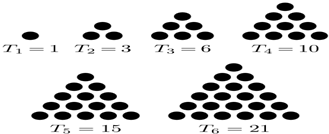    12．小毕喜欢把数描绘成沙滩上的小石子，他照如图所示摆成了正三角形图案，并把每个图案中总的石子个数叫做“三角形数”，记为Tn，则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知离散型随机变量X的分布列为P（X=1）=$\frac{3}{5}$，P（X=2）=$\frac{3}{10}$，P（X=3）=$\frac{1}{10}$，则X的数学期望E（X）=（　　）
    A．$\frac{3}{2}$B．2C．$\frac{5}{2}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知a+b+c＞0，ab+bc+ca＞0，abc＞0，用反证法证明：a，b，c＞0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=2x-$\frac{a}{x}$的定义域为（0，1]（其中a是实数）
    （1）当a=-1时，求函数y=f（x）的值域；
    （2）若函数y=f（x）在定义域上是减函数，求实数a的取值范围；
    （3）求不等式f（x）≥0的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知a∈R，函数f（x）=（-x2+ax）ex，（x∈R，e为自然对数的底数）
    （1）当a=2时，求函数f（x）的单调递增区间．
    （2）函数f（x）是否为R上的单调函数，若是，求出a的取值范围；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数f（x）=$\frac{1}{3}$x3+$\frac{1}{2}$bx2+cx+d在（0，1）内既有极大值又有极小值，求c2+c（1+b）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知tanα=2，求：
    （1）$\frac{2cosα+sinα}{sinα-cosα}$
    （2）sin2α-3sinαcosα的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．抛物线y2=2px（p＞0）的焦点为F，准线为l，A，B是抛物线上的两个动点，且满足∠AFB=$\frac{2π}{3}$．设线段AB的中点M在l上的投影为N，则$\frac{|MN|}{|AB|}$的最大值是$\frac{\sqrt{3}}{3}$．

    查看答案和解析>>

    同步练习册答案