
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
分析 由复数代数形式的乘除运算化简复数$\frac{2-i}{1+i}$,求出在复平面内,复数$\frac{2-i}{1+i}$对应的点的坐标,则答案可求.
解答 解:$\frac{2-i}{1+i}$=$\frac{(2-i)(1-i)}{(1+i)(1-i)}=\frac{1-3i}{2}=\frac{1}{2}-\frac{3}{2}i$,
在复平面内,复数$\frac{2-i}{1+i}$对应的点的坐标为:($\frac{1}{2}$,$-\frac{3}{2}$),位于第四象限.
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.


科目:高中数学 来源: 题型:选择题
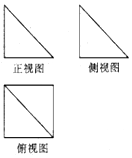 如图所示,某几何体的三视图中,正视图和侧视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )
如图所示,某几何体的三视图中,正视图和侧视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | $1+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
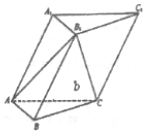 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a,b∈R且a+b=1,则a•b≤$\frac{1}{4}$ | |
| B. | 若a,b∈R,则$\frac{{a}^{2}+{b}^{2}}{2}$≥($\frac{a+b}{2}$)2≥ab恒成立 | |
| C. | $\frac{{x}^{2}+3}{\sqrt{{x}^{2}+1}}$ (x∈R) 的最小值是2$\sqrt{2}$ | |
| D. | x0,y0∈R,x02+y02+x0y0<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com