
分析 根据余弦函数的对称轴公式列方程解出θ.再根据诱导公式和二倍角公式即可求出
解答 解:函数f(x)=3sin$\frac{x}{2}$-4cos$\frac{x}{2}$=5sin($\frac{x}{2}$-φ),其中sinφ=$\frac{4}{5}$,cosφ=$\frac{3}{5}$,
∵函数f(x)=3sin$\frac{x}{2}$-4cos$\frac{x}{2}$的图象关于直线x=θ对称,
∴$\frac{x}{2}$-φ=$\frac{π}{2}$+kπ,
∴x=π+2kπ+2φ=θ,
∴sinθ=sin(π+2kπ+2φ)=-sin2φ=-2sinφcosφ=-2×$\frac{4}{5}$×$\frac{3}{5}$=-$\frac{24}{25}$,
故答案为:-$\frac{24}{25}$.
点评 本题考查了函数的图象变换,三角函数的对称轴公式,属于基础题.


科目:高中数学 来源: 题型:解答题
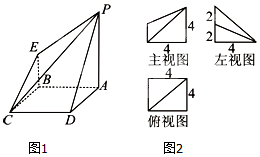 如图是一几何体的直观图、主观图、俯视图、左视图.
如图是一几何体的直观图、主观图、俯视图、左视图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
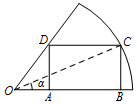 为了废物利用,准备把半径为2,圆心角为$\frac{π}{3}$的扇形铁片余料剪成如图所示的内接矩形ABCD.试用图中α表出内接矩形ABCD的面积S.
为了废物利用,准备把半径为2,圆心角为$\frac{π}{3}$的扇形铁片余料剪成如图所示的内接矩形ABCD.试用图中α表出内接矩形ABCD的面积S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | A∪B=A | C. | A∩B=∅ | D. | A∩∁RB≠∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com