
分析 在①和④中,利用均值不等式求解;在②中,由(a-1)2+(b-1)2≥0,得到a2+b2+2≥2a+2b;在③中,利用作差法知$\sqrt{|a-b|}$≥$\sqrt{a}$-$\sqrt{b}$不恒成立.
解答 解:在①中,∵a>0,b>0,∴(a+b)($\frac{1}{a}$+$\frac{1}{b}$)=2+$\frac{b}{a}+\frac{a}{b}$≥2+2$\sqrt{\frac{b}{a}•\frac{a}{b}}$=4,
当且仅当$\frac{b}{a}=\frac{a}{b}$时取等号,故①正确;
在②中,∵a>0,b>0,(a-1)2+(b-1)2≥0,
∴a2-2a+1+b2-2b+1≥0,
∴a2+b2+2-2a-2b≥0,
∴a2+b2+2≥2a+2b,故②正确;
在③中,∵a>0,b>0,($\sqrt{|a-b|}$)2-($\sqrt{a}$-$\sqrt{b}$)2=|a-b|-a-b+2$\sqrt{ab}$,
当a≥b时,($\sqrt{|a-b|}$)2-($\sqrt{a}$-$\sqrt{b}$)2=|a-b|-a-b+2$\sqrt{ab}$=2$\sqrt{ab}$-2b≥0;
当a<b时,($\sqrt{|a-b|}$)2-($\sqrt{a}$-$\sqrt{b}$)2=|a-b|-a-b+2$\sqrt{ab}$=2$\sqrt{ab}$-2a≥0,
故$\sqrt{|a-b|}$≥$\sqrt{a}$-$\sqrt{b}$恒成立,故③正确;
在④中,∵a>0,b>0,∴$\frac{2ab}{a+b}$≤$\frac{2ab}{2\sqrt{ab}}$=$\sqrt{ab}$.
当且仅当a=b时,取等号,故④错误.
故答案为:①②③.
点评 本题考查基本不等式的性质,涉及不等式的证明,关键是掌握不等式的基本性质、基本不等式的性质.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:选择题

| A. | 2 018×2 014 | B. | 2 018×2 013 | C. | 1 011×2 015 | D. | 1 010×2 012 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
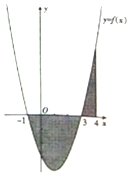
| A. | $\int_{-1}^4{f(x)}dx$ | B. | $-\int_{-1}^4{f(x)}dx$ | ||
| C. | $\int_3^4{f(x)}dx-\int_{-1}^3{f(x)dx}$ | D. | $\int_{-1}^3{f(x)}dx-\int_3^4{f(x)dx}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年降水量(mm) | [200,250] | [250,300] | [300,350] | [350,400] |
| 概率 | 0.30 | 0.21 | 0.14 | 0.08 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
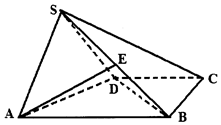 已知四棱锥S-ABCD中,底面是直角梯形,AB=2,BC=CD=1,BC⊥AB,侧面SAD是以∠ASD为直角的等腰三角形,且侧面SAD与底面ABCD垂直.
已知四棱锥S-ABCD中,底面是直角梯形,AB=2,BC=CD=1,BC⊥AB,侧面SAD是以∠ASD为直角的等腰三角形,且侧面SAD与底面ABCD垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com