练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．设f（x）=$\left\{\begin{array}{l}{2-{3}^{x-1}，x＜2}\\{lo{g}_{5}（3x-4），x≥2}\end{array}\right.$，则f（f（3））的值为1．

    分析 先求出∴f（3）=log5（3×3-4）=log55=1，从而f（f（3））=f（1），由此能求出结果．

    解答 解：∵f（x）=$\left\{\begin{array}{l}{2-{3}^{x-1}，x＜2}\\{lo{g}_{5}（3x-4），x≥2}\end{array}\right.$，
    ∴f（3）=log5（3×3-4）=log55=1，
    f（f（3））=f（1）=2-30=1．
    故答案为：1．

    点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．随着人们经济收入的不断增长，个人购买家庭轿车已不再是一种时尚．车的使用费用，尤其是随着使用年限的增多，所支出的费用到底会增长多少，一直是购车一族非常关心的问题．某汽车销售公司作了一次抽样调查，并统计得出某款车的使用年限x与所支出的总费用y（万元）有如表的数据资料：
    使用年限x23456
    总费用y2.23.85.56.57.0
    （1）在给出的坐标系中做出散点图；
    （2）求线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{a}$、$\widehat{b}$；
    （3）估计使用年限为12年时，车的使用总费用是多少？
    （最小二乘法求线性回归方程系数公式$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

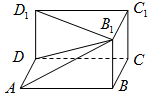    17．长方体ABCD-A1B1C1D1被挖去一个四棱锥后如图所示．已知AB=5，BC=4，BB=3．
    （1）请补全此图的三视图；
     （2）求此几何体的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

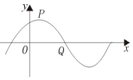    14．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象如图所示，其中点P（1，2）为函数图象的一个最高点，Q（4，0）为函数图象与x轴的一个交点，O为坐标原点．
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）将函数y=f（x）的图象向右平移2个单位得到y=g（x）的图象，求函数h（x）=f（x）•g（x）图象的对称中心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知x，y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x-2y+2≤0}\\{y≤2}\end{array}\right.$，则z=2x-3y的最小值为-4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．设n∈N+，由计算得f（2）=$\frac{3}{2}$，f（4）＞2，f（8）＞$\frac{5}{2}$，f（32）＞$\frac{7}{2}$，观察上述结果，可推出一般的结论为f（2n）$≥\frac{n+2}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知$\overrightarrow a，\overrightarrow b$是夹角为60°的两个单位向量，则当实数t∈[-1，1]，$|\overrightarrow a+t\overrightarrow b|$的最大值为$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知数列满足a1=1，an+1=2an+1（n∈N*）．则通项公式为an=2n-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．求下列函数的定义域：
    （1）y=（27-3x）${\;}^{\frac{1}{2}}$；
    （2）y=（log${\;}_{\frac{1}{2}}$（x-1））${\;}^{-\frac{1}{2}}$．

    查看答案和解析>>

    同步练习册答案