
分析 (Ⅰ)连接RF,PF,利用等角的余角相等,证明∠PRA=∠PQF,即可证明AR∥FQ;
(Ⅱ)利用△PQF的面积是△ABF的面积的两倍,求出N的坐标,利用点差法求AB中点的轨迹方程.
解答 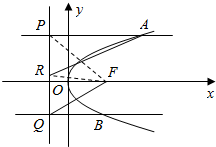 (Ⅰ)证明:连接RF,PF,
(Ⅰ)证明:连接RF,PF,
由AP=AF,BQ=BF及AP∥BQ,得∠AFP+∠BFQ=90°,
∴∠PFQ=90°,
∵R是PQ的中点,
∴RF=RP=RQ,
∴△PAR≌△FAR,
∴∠PAR=∠FAR,∠PRA=∠FRA,
∵∠BQF+∠BFQ=180°-∠QBF=∠PAF=2∠PAR,
∴∠FQB=∠PAR,
∴∠PRA=∠PQF,
∴AR∥FQ.
(Ⅱ)设A(x1,y1),B(x2,y2),
F($\frac{1}{2}$,0),准线为 x=-$\frac{1}{2}$,
S△PQF=$\frac{1}{2}$|PQ|=$\frac{1}{2}$|y1-y2|,
设直线AB与x轴交点为N,
∴S△ABF=$\frac{1}{2}$|FN||y1-y2|,
∵△PQF的面积是△ABF的面积的两倍,
∴2|FN|=1,∴xN=1,即N(1,0).
设AB中点为M(x,y),由$\left\{\begin{array}{l}{{{y}_{1}}^{2}=2{x}_{1}}\\{{{y}_{2}}^{2}=2{x}_{2}}\end{array}\right.$得${{y}_{1}}^{2}-{{y}_{2}}^{2}$=2(x1-x2),
又$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{y}{x-1}$,
∴$\frac{y}{x-1}$=$\frac{1}{y}$,即y2=x-1.
∴AB中点轨迹方程为y2=x-1.
点评 本题考查抛物线的方程与性质,考查轨迹方程,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
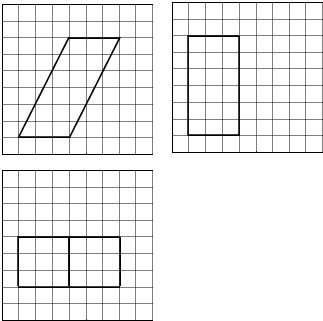
| A. | 18+36$\sqrt{5}$ | B. | 54+18$\sqrt{5}$ | C. | 90 | D. | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{2}$个单位长度 | B. | -π个单位长度 | C. | π个单位长度 | D. | $\frac{π}{2}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com