
分析 利用三角函数恒等变换的应用化简已知可得cos(A-B)+sin(A+B)=2,由cos(A-B),sin(A+B)的范围,解得cos(A-B)=1,sin(A+B)=1,解得A=B=45°,C=90°,利用正弦定理化简可得$\frac{a+b}{c}$=$\frac{sinA+sinB}{sinC}$,即可得解.
解答 解:在△ABC中,∵cosA+sinA-$\frac{2}{cosB+sinB}$=0,
∴(cosA+sinA)(cosB+sinB)=2,
∴cosAcosB+sinAsinB+sinAcosB+sinBcosA=2,
∴cos(A-B)+sin(A+B)=2,
∵cos(A-B)∈[-1,1];sin(A+B)∈[-1,1],
∴当二者和为2时,只能是二者均为1,
即cos(A-B)=1,sin(A+B)=1,
∵A、B、C为△ABC内角,
∴A-B=0,A+B=90°,
∴解得A=B=45°,
∴C=180°-45°-45°=90°,
∴$\frac{a+b}{c}$=$\frac{sinA+sinB}{sinC}$=$\frac{{\sqrt{2}}}{2}$+$\frac{{\sqrt{2}}}{2}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题主要考查了正弦定理,三角函数恒等变换的应用,三角函数的图象和性质在解三角形中的应用,考查了转化思想,属于中档题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
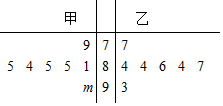 如图是七位评委为甲、乙两名比赛歌手打出的分数的茎叶图(其中m为数字0-9中的一个),甲、乙两名选手得分的平均数分别为a1,a2,若a1=a2,则m=( )
如图是七位评委为甲、乙两名比赛歌手打出的分数的茎叶图(其中m为数字0-9中的一个),甲、乙两名选手得分的平均数分别为a1,a2,若a1=a2,则m=( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | π | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com