
分析 由已知可得点A,F1,F2的坐标,再利用数量积运算法则和点P的纵坐标的取值范围即可得出最大值.
解答 解:由椭圆$C:\frac{x^2}{4}+\frac{y^2}{3}=1$可得a2=4,b2=3,c=$\sqrt{{a}^{2}-{b}^{2}}$=1,
可得F1(-1,0),F2(1,0),
由AF2⊥F1F2,令x=1,可得y=±$\sqrt{3}$•$\sqrt{1-\frac{1}{4}}$=±$\frac{3}{2}$,可设A(1,$\frac{3}{2}$),
设P(m,n),则$\frac{{m}^{2}}{4}$+$\frac{{n}^{2}}{3}$=1,
又-$\sqrt{3}$≤n≤$\sqrt{3}$,
则$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}A}$=(m+1,n)•(0,$\frac{3}{2}$)=$\frac{3}{2}$n≤$\frac{3\sqrt{3}}{2}$.
可得$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}A}$的最大值为$\frac{3\sqrt{3}}{2}$.
故答案为:$\frac{3\sqrt{3}}{2}$.
点评 本题考查了椭圆的标准方程及其性质、数量积运算等基础知识与基本技能方法,属于基础题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4或$-\frac{17}{2}$ | C. | -4或4 | D. | -4或4或-$\frac{17}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
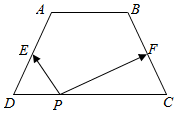 如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,那么实数λ的取值范围为(-$\frac{9}{20}$,-$\frac{1}{4}$).
如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,那么实数λ的取值范围为(-$\frac{9}{20}$,-$\frac{1}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
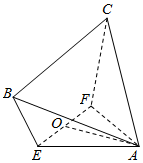 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com