
| A. | 一解 | B. | 两解 | C. | 一解或两解 | D. | 无解 |
分析 (法一)利用正弦定理和边角关系可判断出此三角形解的情况;
(法二)由题意画出图形,再结合条件可此三角形解的情况.
解答 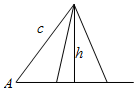 解:(法一)由正弦定理得$\frac{a}{sinA}=\frac{c}{sinC}$,
解:(法一)由正弦定理得$\frac{a}{sinA}=\frac{c}{sinC}$,
则sinC=$\frac{c•sinA}{a}$=$\frac{\sqrt{3}×\frac{1}{2}}{1}$=$\frac{\sqrt{3}}{2}$,
又0°<C<180°,则C=60°或120°,
因为c>a,A=30°,所以C=60°或120°都成立,
所以此三角形有两解
(法二)因为A=30°,c=$\sqrt{3}$,a=1,如图:
所以h=csinA=$\sqrt{3}×\frac{1}{2}$=$\frac{\sqrt{3}}{2}$,
又$\frac{\sqrt{3}}{2}$<1<$\sqrt{3}$,则此三角形有两解,
故选:B.
点评 本题考查利用正弦定理、边角关系,或结合图形判断出三角形解的情况,利用图形更直观,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
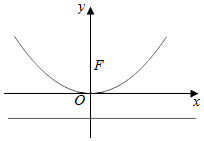 已知点F为抛物线E:x2=4y的焦点,直线l为准线,C为抛物线上的一点(C在第一象限),以点C为圆心,|CF|为半径的圆与y轴交于D,F两点,且△CDF为正三角形.
已知点F为抛物线E:x2=4y的焦点,直线l为准线,C为抛物线上的一点(C在第一象限),以点C为圆心,|CF|为半径的圆与y轴交于D,F两点,且△CDF为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
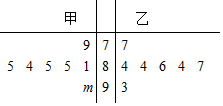 如图是七位评委为甲、乙两名比赛歌手打出的分数的茎叶图(其中m为数字0-9中的一个),甲、乙两名选手得分的平均数分别为a1,a2,若a1=a2,则m=( )
如图是七位评委为甲、乙两名比赛歌手打出的分数的茎叶图(其中m为数字0-9中的一个),甲、乙两名选手得分的平均数分别为a1,a2,若a1=a2,则m=( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com