
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
分析 【法一】根据复数的代数形式的运算法则,求出z,再计算模长|z|;
【法二】根据复数模长公式,对等式直接求模即可.
解答 解:【法一】∵(1-i)z=$\frac{1+3i}{1-2i}$,
∴z=$\frac{1+3i}{(1-2i)(1-i)}$=$\frac{1+3i}{-1-3i}$=-1,
∴|z|=1.
【法二】∵(1-i)z=$\frac{1+3i}{1-2i}$,
∴|1-i|•|z|=$\frac{|1+3i|}{|1-2i|}$,
即$\sqrt{2}$•|z|=$\frac{\sqrt{10}}{\sqrt{5}}$,
解得|z|=1.
故选:A.
点评 本题考查了复数代数形式的运算以及复数模的计算问题,是基础题目.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
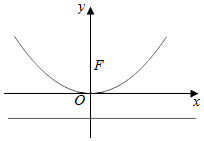 已知点F为抛物线E:x2=4y的焦点,直线l为准线,C为抛物线上的一点(C在第一象限),以点C为圆心,|CF|为半径的圆与y轴交于D,F两点,且△CDF为正三角形.
已知点F为抛物线E:x2=4y的焦点,直线l为准线,C为抛物线上的一点(C在第一象限),以点C为圆心,|CF|为半径的圆与y轴交于D,F两点,且△CDF为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | π | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com