
| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:解答题
| 非体育迷 | 体育迷 | 总计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 总计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (-∞,4) | C. | [4,+∞) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
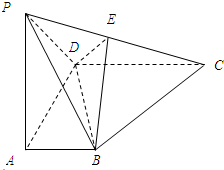 如图,四棱锥P-ABCD底面为一直角梯形,AB⊥AD,CD⊥AD,CD=2AB,PA⊥面ABCD,E为PC中点
如图,四棱锥P-ABCD底面为一直角梯形,AB⊥AD,CD⊥AD,CD=2AB,PA⊥面ABCD,E为PC中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
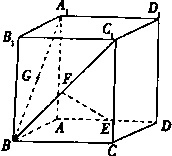 如图,在单位正方体A1B1C1D1-ABCD中,E,F,G分别是AD,BC1,A1B的中点.
如图,在单位正方体A1B1C1D1-ABCD中,E,F,G分别是AD,BC1,A1B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M={2,3},S={(2,3)} | |
| B. | M={π},S={3.14} | |
| C. | M={0},S=∅ | |
| D. | M={1,2,3,…,n-1,n},S={前n个非零自然数} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com