
���� ��Ϊ�����Լ���Ľ�����һ����ѧͳ����������ʵ�������е�ȷ�����Ǵ��ڲ���ģ�����жϼ��ɣ�
��� �⣺�����Լ���Ľ�����һ����ѧͳ����������ʵ�������е�ȷ�����Ǵ��ڲ���ģ�
����100����������������99���˻��зβ�����Ȼ����
����1�������̣���ô�������99%�ĸ��ʻ��зβ�������ͳ�ƣ�����ȷ�ģ�
����100����������һ���л��β����ˣ���Ȼ����
����100���������п���û��һ�����β����ˣ�Ҳ�п��ܣ�����ȷ��
�ʴ�Ϊ�ڢܣ�
���� �����˶����Լ���ĸ���Ͷ���ѧͳ�Ƶ����⣮���ڻ������ͣ�Ӧ�μǣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
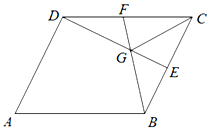 ��ͼ���߳�Ϊ2������ABCD�У���A=60�㣬E��F�ֱ���BC��DC���е㣬GΪ BF��DE�Ľ��㣬��$\overrightarrow{AB}=\overrightarrow a$��$\overrightarrow{AD}=\overrightarrow b$��
��ͼ���߳�Ϊ2������ABCD�У���A=60�㣬E��F�ֱ���BC��DC���е㣬GΪ BF��DE�Ľ��㣬��$\overrightarrow{AB}=\overrightarrow a$��$\overrightarrow{AD}=\overrightarrow b$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
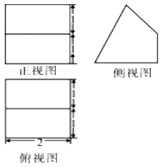
| A�� | 3cm3 | B�� | 5cm3 | C�� | 4cm3 | D�� | 6cm3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
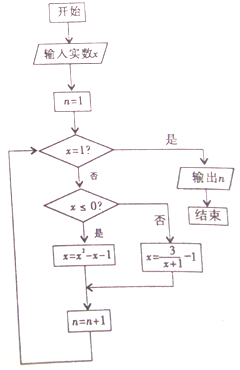
 ������ʽ��x2+x+1��nչ������n=0��1��2��3����ʱ���õ����µ�ʽ��
������ʽ��x2+x+1��nչ������n=0��1��2��3����ʱ���õ����µ�ʽ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com