练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．将三项式（x2+x+1）n展开，当n=0，1，2，3，…时，得到以下等式：
    （x2+x+1）0=1
    （x2+x+1）1=x2+x+1
    （x2+x+1）2=x4+2x3+3x2+2x+1
    （x2+x+1）3=x6+3x5+6x4+7x3+6x2+3x+1
    …
    观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数（不足3数的，缺少的数计为0）之和，第k行共有2k+1个数．若在（1+ax）（x2+x+1）5的展开式中，x8项的系数为67，则实数a值为$\frac{26}{15}$．

    分析 由题意可得广义杨辉三角形第5行为1，5，15，30，45，51，45，30，15，5，1，所以（1+ax）（x2+x+1）5的展开式中，x8项的系数为15+30a=75，即可求出实数a的值．

    解答 解：由题意可得广义杨辉三角形第5行为1，5，15，30，45，51，45，30，15，5，1，
    所以（1+ax）（x2+x+1）5的展开式中，x8项的系数为15+30a=67，
    所以a=$\frac{26}{15}$．
    故答案为：$\frac{26}{15}$．

    点评 本题考查二项式定理的运用以及归纳推理，解题的关键在于发现所给等式的系数变化的规律．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．在研究吸烟与患有肺病的关系中，通过收集数据、整理分析数据得“吸烟与患有肺病有关”的结论，并且有99%以上的把握认为这个结论是成立的，则有以下说法：
    ①在100个吸烟者中至少有99个人患有肺病；
    ②若1个人吸烟，那么这个人有99%的概率患有肺病；
    ③在100个吸烟者中一定有患肺病的人；
    ④在100个吸烟者中可能没有一个患肺病的人．你认为正确的说法是②④．
    （填上你认为正确的所有说法的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．空间四边形ABCD的四个顶点都在同一球面上，E、F分别是AB、CD的中点，且EF⊥AB，EF⊥CD，若AB=8，CD=EF=4，则该球的半径等于（　　）
    A．$\frac{{65\sqrt{2}}}{16}$B．$\frac{{65\sqrt{2}}}{8}$C．$\frac{{\sqrt{65}}}{2}$D．$\sqrt{65}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知圆C：（x-a）2+（y-2）2=4（a＞0）与直线l：x-y+3=0交于两点A，B．
    （1）当直线l被圆C截得的弦长为$2\sqrt{2}$时，求a的值；
    （2）若圆上存在点P，满足$\overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{CP}$，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知 y=f （ x ） 是定义在 R 上的偶函数，且当 x∈（-∞，0），f （ x ）+xf'（ x ）＜0成立（ f'（ x ） 是函数 f （ x） 的导数），若 a=$\frac{1}{2}$f （log2$\sqrt{2}$ ），b=（ln 2 ） f （ln 2 ），c=2f （-2 ），则 a，b，c 的大小关系是（　　）
    A．a＞b＞cB．b＞a＞cC．c＞a＞bD．a＞c＞b

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知关于x的方程$\frac{{x}^{2}+2}{x（lnx+k）+2k}$=1在x∈[$\frac{1}{2}$，+∞]上有两个不相等的实数根，则实数k的取值范围为（1，$\frac{9+2ln2}{10}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．执行如图所示的程序框图，输入θ=$\frac{π}{180}$，n=1，输出的结果是（　　）
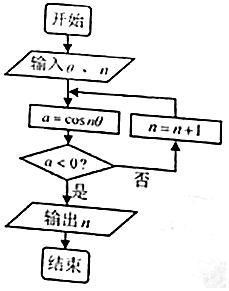
    A．90B．91C．180D．270

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．如图，给出的是$1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{99}$的值的一个程序框图，判断框内应填入的条件是（　　）
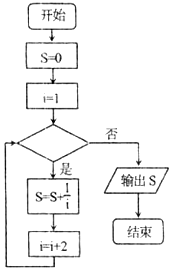
    A．i＜99B．i≤99C．i＞99D．i≥99

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知集合$A=\left\{{x\left|{y=\sqrt{{3^x}-3}}\right.}\right\}$，集合$B=\left\{{x\left|{y=\sqrt{{{log}_{0.5}}x+1}}\right.}\right\}$．
    （1）求A∩B；
    （2）集合C={x|a-2≤x≤2a-1}，且C∪（A∩B）=C，求实数a 的取值范围．

    查看答案和解析>>

    同步练习册答案