练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．天干地支纪年法，源于中国．中国自古便有十天干与十二地支．
    十天干：甲、乙、丙、丁、戊、己、庚、辛、壬、癸；
    十二地支：子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥．
    天干地支纪年法是按顺序以一个天干和一个地支相配，排列起来，天干在前，地支在后，天干由“甲”起，地支由“子”起，比如第一年为“甲子”，第二年为“乙丑”，第三年为“丙寅”，…，以此类推．排列到“癸酉”后，天干回到“甲”重新开始，即“甲戌”，“乙亥”，之后地支回到“子”重新开始，即“丙子”，…，以此类推．
    已知2017年为丁酉年，那么到改革开放100年时，即2078年为戊戌年．

    分析 由题意可得数列天干是以10为等差的等差数列，地支是以12为公差的等差数列，以2017年的天干和地支分别为首项，即可求出答案．

    解答 解：天干是以10为构成的等差数列，地支是以12为公差的等差数列，
    从2017年到2078年经过61年，且2017年为丁酉年，以2017年的天干和地支分别为首项，
    则61÷10=6余1，则2078的天干为戊，
    61÷12=5余1，则戊的地支为戌，
    故答案为：戊戌

    点评 本题考查了等差数列在实际生活中的应用，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    19．△ABC的外接圆圆心为P，若点P满足$\overrightarrow{AP}$=$\frac{2}{5}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），则cos∠BAC=$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知过点M（1，-1）的直线l与椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$相交于A，B两点，若点M是AB的中点，则直线l的方程为3x-4y-7=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若定义在R上的偶函数f（x）满足f（x+1）=-f（x），且在区间[0，1]上单调递减，则将$f（{-\frac{5}{2}}）$，f（7），f（4）从小到大顺序排列为$f（7）＜f（{-\frac{5}{2}}）＜f（4）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．某次数学考试的第一大题由10道四选一的选择题构成，要求考生从A，B，C，D中选出其中一项作为答案，每题选择正确得5分，选择错误不得分．以下是甲、乙、丙、丁四位考生的答案及甲、乙、丙三人的得分结果：
    题1题2题3题4题5题6题7题8题9题10得分
    甲CBDDACDCAD35
    乙CBCDBCABDC35
    丙CADDADABAC40
    丁CADDBCABAC？
    据此可以推算考生丁的得分是40．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．如图所示的程序框图，当输入x的值为3时，则其输出的结果是1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知$tan（{π-α}）=\frac{3}{4}，α∈（{\frac{π}{2}，π}）$，则cosα=（　　）
    A．$-\frac{4}{5}$B．$\frac{4}{5}$C．$-\frac{3}{5}$D．$\frac{3}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．向量$\overrightarrow m=（{\sqrt{3}sin\frac{x}{4}，1}），\overrightarrow n=（{cos\frac{x}{4}，{{cos}^2}\frac{x}{4}}）$，记$f（x）=\overrightarrow m•\overrightarrow n$．
    （1）若f（x）=1，求$cos（{x+\frac{π}{3}}）$的值；
    （2）在锐角△ABC中，角A，B，C的对边分别是a，b，c，且满足（2a-c）cosB=bcosC，求f（2A）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

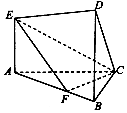    14．在如图所示的几何体中，EA⊥平面ABC，DB∥EA，AC⊥BC，且BC=BD=3，AE=2，AC=3$\sqrt{2}$，AF=2FB
    （1）求证：CF⊥EF；
    （2）求二面角D-CE-F的余弦值．

    查看答案和解析>>

    同步练习册答案