练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．命题p：方程x2+mx+1=0有两个不等的正实数根，
    命题q：方程4x2+4（m+2）x+1=0无实数根．若“p且q”为真命题，求m的取值范围．

    分析 求出命题p、q为真时，m的取值范围，再求交集

    解答 解：“p且q”为真命题，
    当p为真命题时，则$\left\{\begin{array}{l}△={m^2}-4＞0\\{x_1}+{x_2}=-m＞0\\{x_1}{x_2}=1＞0\end{array}\right.$，得m＜-2；
    当q为真命题时，则△=16（m+2）2-16＜0，得-3＜m＜-1，
    若“p且q”为真命题，则$\left\{\begin{array}{l}{m＜-2}\\{-3＜m＜-1}\end{array}\right.$⇒-3＜m＜-2．
    ∴m的取值范围为：[-3，-2]．

    点评 本题考查了复合命题真假的应用．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．已知△ABC，$A（{1，1}），B（{1，3}），C（{1+\sqrt{3}，2}）$，若点（x，y）在三角形内部（不包含边界），则z=-2x+y的取值范围是（　　）
    A．$（{-\sqrt{3}，-1}）$B．（-1，1）C．$（{-2\sqrt{3}，1}）$D．$（{-1，\sqrt{3}}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．△ABC中，若4sinA+2cosB=4，$\frac{1}{2}sinB+cosA=\frac{{\sqrt{3}}}{2}$，则角C=$\frac{π}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．若f（x）=$\left\{\begin{array}{l}{x-2，x≥10}\\{f（x+6），x＜10}\end{array}\right.$则f（5）的值（　　）
    A．3B．5C．7D．9

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

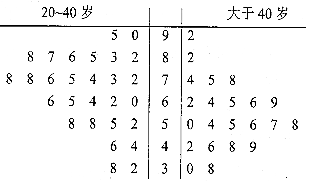
    15．某公司即将推车一款新型智能手机，为了更好地对产品进行宣传，需预估市民购买该款手机是否与年龄有关，现随机抽取了50名市民进行购买意愿的问卷调查，若得分低于60分，说明购买意愿弱；若得分不低于60分，说明购买意愿强，调查结果用茎叶图表示如图所示．

    （1）根据茎叶图中的数据完成2×2列联表，并判断是否有95%的把握认为市民是否购买该款手机与年龄有关？
    购买意愿强购买意愿弱合计
    20-40岁
    大于40岁
    合计
    （2）从购买意愿弱的市民中按年龄进行分层抽样，共抽取5人，从这5人中随机抽取2人进行采访，求这2人都是年龄大于40岁的概率．
    附：${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
    P（K2≥k0）0.1000.0500.0100.001
    k02.7063.8416.63510.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知函数f （x）=lg$\frac{10}{\sqrt{1+4{x}^{2}}-2x}$，则f （2017）+f （-2017）=（　　）
    A．0B．2C．20D．4034

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在研究色盲与性别的关系调查中，调查了男性500人，其中有50人患色盲，调查的500个女性中10人患色盲，
    （1）根据以上的数据建立一个2*2的列联表；
    （2）能否在犯错误的概率不超过0.001的前提下，认为“性别与患色盲有关系”？说明你的理由．（注：P（K2≥10.828）=0.001）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

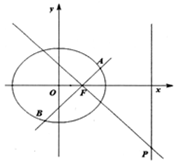    9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）．
    （1）若椭圆的两个焦点与一个短轴顶点构成边长为2的正三角形，求椭圆的标准方程；
    （2）过右焦点（c，0）的直线l与椭圆C交于A、B两点，过点F作l的垂线，交直线x=$\frac{{a}^{2}}{c}$于P点，若$\frac{|PF|}{|AB|}$的最小值为$\frac{b}{a}$，试求椭圆C率心率e的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．在△ABC中，三内角A、B、C的对边分别为a、b、c，且$\frac{c-b}{{\sqrt{2}c-a}}=\frac{sinA}{sinB+sinC}$
    （I）求角B的大小，
    （Ⅱ）设$\overrightarrow{m}=（sinA+cosA，1），\overrightarrow{n}=（2，cos（\frac{π}{2}-2A））$，求$\overrightarrow{m}•\overrightarrow{n}$的取值范围．

    查看答案和解析>>

    同步练习册答案