
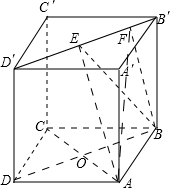
 如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF=
如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF=| 1 |
| 2 |
| A、AC⊥BE |
| B、EF∥平面ABCD |
| C、三棱锥A-BEF的体积为定值 |
| D、异面直线AE,BF所成角为定值 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
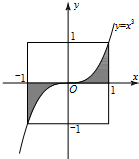 如图,设D是图中边长为2的正方形区域,E是函数y=x3的图象与x轴及x=±1围成的阴影区域.向D中随机投一点,则该点落入E中的概率为( )
如图,设D是图中边长为2的正方形区域,E是函数y=x3的图象与x轴及x=±1围成的阴影区域.向D中随机投一点,则该点落入E中的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 为监测幼儿身体发育状况,某幼儿园对“大班”的100名幼儿的体重做了测量,并根据所得数据画出了频率分布直方图,如图所示.则体重在[18,20](单位kg)的幼儿人数为( )
为监测幼儿身体发育状况,某幼儿园对“大班”的100名幼儿的体重做了测量,并根据所得数据画出了频率分布直方图,如图所示.则体重在[18,20](单位kg)的幼儿人数为( )| A、10 | B、15 | C、30 | D、75 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 6 |
| 3 |
| NA |
| 7 |
| 5 |
| NB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MB |
| AM |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com