
已知函数f(x)=x|x-a|+2x-3
(1)当a=4,2≤ x≤5时,求函数f(x)的最大值和最小值;(2)当xÎ[1,2]时,f(x)≤2x-2恒成立,求实数a的取值范围.
x≤5时,求函数f(x)的最大值和最小值;(2)当xÎ[1,2]时,f(x)≤2x-2恒成立,求实数a的取值范围.
(1)当a=4时,f(x)=x|x-4|+2x-3;①当2≤x<4时,f(x)=x(4-x)+2x-3=-x2+6x-3,
当x=2时,f(x)min=5;当x=3时,f(x)max=6 2分②当4≤x≤5时,f(x)=x(x-4)+2x-3=x2-2x-3=(x-1)2-4,当x=4时,f(x)min=5;当x=5时,f(x)max=12 4分
综上可知,函数f(x)的最大值为12,最小值为5. 6分
(2)若x≥a,原不等式化为f(x)= x2-ax≤1,即a≥x-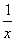 在xÎ[1,2]上恒成立,∴a≥(x-
在xÎ[1,2]上恒成立,∴a≥(x-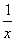 )max,即a≥
)max,即a≥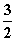 . 若x<a,原不等式化为f(x)=-x2+ax≤1,即a≤x+
. 若x<a,原不等式化为f(x)=-x2+ax≤1,即a≤x+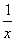 在xÎ[1,2]上恒成立,∴a≤(x-
在xÎ[1,2]上恒成立,∴a≤(x-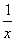 )min,即a≤2. 10分
)min,即a≤2. 10分
综上可知,a的取值范围为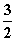 ≤a≤2. 12分
≤a≤2. 12分


科目:高中数学 来源: 题型:
对于函数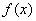 ,若存在区间
,若存在区间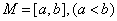 ,使得
,使得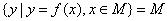 ,则称区间M为函数
,则称区间M为函数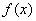 的一个“稳定区间”,现有四个函数:
的一个“稳定区间”,现有四个函数:
①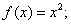 ②
②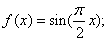 ③
③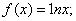 ④
④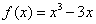
其中存在“稳定区间”的函数为 ( )
A.① B.①② C.①②③ D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com