练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    一个大型喷水池的中央有一个强大喷水柱，为了测量喷水柱喷出的水柱的高度，某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°，沿点A向北偏东30°前进100 m到达点B，在B点测得水柱顶端的仰角为30°，则水柱的高度是(　　)

    A．50 m         B．100 m      C．120 m        D．150 m


    A　设水柱高度是h m，水柱底端为C，则在△ABC中，A＝60°，AC＝h，AB＝100，BC＝h，根据余弦定理得，(h)2＝h2＋1002－2·h·100·cos 60°，即h2＋50h－5 000＝0，即(h－50)(h＋100)＝0，即h＝50，故水柱的高度是50 m.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    2013年全球经济开始转暖，据统计某地区1月、2月、3月的用工人数分别为0.2万人，0.4万人和0.76万人，则该地区这三个月的用工人数y万人关于月数x的函数关系近似的是(　　)

    A．y＝0.2x                         B．y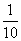＝(x2＋2x)

    C．y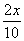＝                          D．y＝0.2＋log16x

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a＝(1,0)，b＝(2,1)．求：

    (1)|a＋3b|；

    (2)当k为何实数时，ka－b与a＋3b平行，平行时它们是同向还是反向？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，若lg sin A－lg cos B－lg sin C＝lg 2，则△ABC的形状是(　　)

    A．直角三角形                                         B．等腰直角三角形

    C．等边三角形                                         D．等腰三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，角A、B、C的对边分别为a、b、c ，且a2－(b－c)2＝(2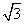－)bc，sin Asin B＝cos2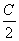，BC边上的中线AM的长为.

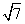    (1)求角A和角B的大小；

    (2)求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在海岸A处，发现北偏东45°方向，距离A处(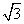－1)海里的B处有一艘走私船；在A处北偏西75°方向，距离A处2海里的C处的缉私船奉命以10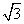海里/小时的速度追截走私船．同时，走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜，问缉私船沿什么方向能最快追上走私船？最少要花多少时间？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知平面内一点P及△ABC，若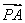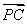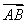＋＋＝，则点P与△ABC的位置关系是(　　)

    A．点P在线段AB上                               B．点P在线段BC上

    C．点P在线段AC上                               D．点P在△ABC外部

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知|a|＝4，|b|＝8，a与b的夹角是120°.

    (1)计算：①|a＋b|，②|4a－2b|；

    (2)当k为何值时，(a＋2b)⊥(ka－b)?

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等差数列{an}满足a2＝3，Sn－Sn－3＝51(n>3)，Sn＝100，则n的值为(　　)

    A．8                                       B．9

    C．10                                     D．11

    查看答案和解析>>

    同步练习册答案