练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．如图，在Rt△ABC中，E为BC边上一点，且$\overrightarrow{EB}$=$3\overrightarrow{CE}$，若向量$\overrightarrow{AE}$利用$\overrightarrow{AB}$，$\overrightarrow{AC}$表示，则$\overrightarrow{AE}$=$\frac{1}{4}\overrightarrow{AB}$$+\frac{3}{4}\overrightarrow{AC}$．

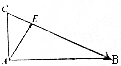
    分析 根据向量减法的几何意义及$\overrightarrow{EB}=3\overrightarrow{CE}$便可得出$\overrightarrow{AB}-\overrightarrow{AE}=3（\overrightarrow{AE}-\overrightarrow{AC}）$，从而进行向量的数乘运算便可解出向量$\overrightarrow{AE}$，即用$\overrightarrow{AB}，\overrightarrow{AC}$表示出$\overrightarrow{AE}$．

    解答 解：由$\overrightarrow{EB}=3\overrightarrow{CE}$得：$\overrightarrow{AB}-\overrightarrow{AE}=3（\overrightarrow{AE}-\overrightarrow{AC}）$；
    ∴$4\overrightarrow{AE}=\overrightarrow{AB}+3\overrightarrow{AC}$；
    ∴$\overrightarrow{AE}=\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$．
    故答案为：$\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$．

    点评 考查向量减法的几何意义，以及向量的数乘运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．若S1=${∫}_{0}^{1}$（ex-1）dx，S2=${∫}_{0}^{1}$xdx，S3=${∫}_{0}^{1}$sinxdx，则（　　）
    A．S2＞S3＞S1B．S1＞S3＞S2C．S2＞S1＞S3D．S1＞S2＞S3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知集合A={x|x2-3x+2≥0}，B={x|x≥t}．若A∪B=A，则实数t的取值范围为[2，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

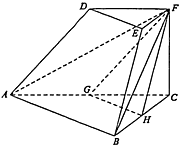    8．如图，在三棱台DEF-ABC中，已知底面ABC是以AB为斜边的直角三角形，FC⊥底面ABC，AB=2DE，G，H分别为AC，BC的中点．
    （1）求证：平面ABED∥平面GHF；
    （2）若BC=CF=$\frac{1}{2}$AB=1，求棱锥F-ABHG的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在线性回归模型中，分别选择了4个不同的模型，它们的相关指数R2依次为0.36、0.95、0.74、0.81，其中回归效果最好的模型的相关指数R2为（　　）
    A．0.95B．0.81C．0.74D．0.36

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=lnx+ax2+1的图象在点（1，f（1））处切线的斜率为3．
    （1）求实数a的值；
    （2）证明：存在正实数λ，使得|$\frac{1-x}{f（x）-lnx}$|≤λ恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．定义在R上的函数f（x）满足对任意x，y∈R恒有f（xy）=f（x）+f（y），且f（x）不恒为0，
    （1）求f（1）和f（-1）的值；
    （2）试判断f（x）的奇偶性，并加以证明；
    （3）若x≥0时f（x）为增函数，求满足不等式f（x+1）-f（2-x）≤0的x取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．将函数f（x）=sin4x-$\sqrt{3}$cos4x的图象上所有点的横坐标伸长到原来的2倍（纵坐标保持不变），再向左平移$\frac{π}{12}$个单位长度，得到函数g（x）的图象，则下列说法不正确的是（　　）
    A．g（x）的最大值为2B．g（x）在[0，$\frac{π}{2}$]上是增函数
    C．函数g（x）的图象关于直线x=$\frac{π}{3}$对称D．函数g（x）的图象关于点（$\frac{π}{12}$，0）对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=ex-x，g（x）=ax2+1，其中e为自然对数的底数．
    （1）若函数F（x）=f（x）-g（x）的导函数F′（x）在[0，+∞）上是增函数，求实数a的最大值；
    （2）求证：f（1）+f（$\frac{1}{2}$）+f（$\frac{1}{3}$）+…+f（$\frac{1}{n}$）＞$\frac{n（2n+3）}{2（n+1）}$，n∈N+．

    查看答案和解析>>

    同步练习册答案