练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    [2013·重庆高考]已知函数f(x)＝ax3＋bsinx＋4(a，b∈R)，f(lg(log210))＝5，则f(lg(lg2))＝(　　)

    A.－5 B.－1 C.3 D.4

     

    C

    【解析】∵f(x)＝ax3＋bsinx＋4，　①

    ∴f(－x)＝a(－x)3＋bsin(－x)＋4，

    即f(－x)＝－ax3－bsinx＋4，　②

    ①＋②得f(x)＋f(－x)＝8，　③

    又∵lg(log210)＝lg()＝lg(lg2)－1＝－lg(lg2)，

    ∴f(lg(log210))＝f(－lg(lg2))＝5，

    又由③式知

    f(－lg(lg2))＋f(lg(lg2))＝8，

    ∴5＋f(lg(lg2))＝8，

    ∴f(lg(lg2))＝3.故选C.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015数学一轮复习迎战高考：3-8解三角形应用举例（解析版） 题型：填空题

    [2012·福建高考]已知△ABC的三边长成公比为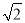的等比数列，则其最大角的余弦值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015数学一轮复习迎战高考：2-9函数模型及其应用（解析版） 题型：选择题

    [2014·长沙模拟]已知某生产厂家的年利润y(单位：万元)与年产量x(单位：万件)的函数关系式为y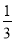＝－x3＋81x－234，则使该生产厂家获取最大年利润的年产量为(　　)

    A.13万件 B.11万件 C.9万件 D.7万件

     

    查看答案和解析>>

    科目：高中数学 来源：2015数学一轮复习迎战高考：2-5指数及指数函数（解析版） 题型：填空题

    [2014·亳州模拟]若函数f(x)＝ax(a＞0，a≠1)在[－1,2]上的最大值为4，最小值为m，且函数g(x)＝(1－4m)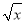在[0，＋∞)上是增函数，则a＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2015数学一轮复习迎战高考：2-4二次函数与幂函数（解析版） 题型：选择题

    [2014·福州质检]设二次函数f(x)＝ax2－2ax＋c在区间[0,1]上单调递减，且f(m)≤f(0)，则实数m的取值范围是(　　)

    A.(－∞，0] B.[2，＋∞)

    C.(－∞，0]∪[2，＋∞) D.[0,2]

     

    查看答案和解析>>

    科目：高中数学 来源：2015数学一轮复习迎战高考：2-2函数的单调性与最值（解析版） 题型：选择题

    [2013·吉林调研]已知定义在R上的函数f(x)满足f(x)＋f(－x)＝0，且在(－∞，0)上单调递增，如果x1＋x2＜0且x1x2＜0，则f(x1)＋f(x2)的值(　　)

    A.可能为0 B.恒大于0

    C.恒小于0 D.可正可负

     

    查看答案和解析>>

    科目：高中数学 来源：2015数学一轮复习迎战高考：2-1函数的概念、定义域和值域（解析版） 题型：选择题

    [2013·湖北荆门期末]函数f(x)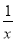＝ln(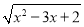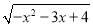＋)的定义域为(　　)

    A.(－∞，－4]∪(2，＋∞)

    B.(－4,0)∪(0,1)

    C.[－4,0)∪(0,1]

    D.[－4,0)∪(0,1)

     

    查看答案和解析>>

    科目：高中数学 来源：2015数学一轮复习迎战高考：2-10导数的概念及运算（解析版） 题型：填空题

    [2013·江西高考]设函数f(x)在(0，＋∞)内可导，且f(ex)＝x＋ex，则f′(1)＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2015数学一轮复习迎战高考：1-1集合的概念与运算（解析版） 题型：选择题

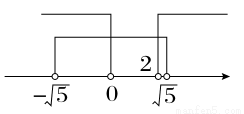
    [2013·课标全国卷Ⅰ]已知集合A＝{x|x2－2x＞0}，B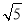＝{x|－＜x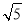＜}，则(　　)

    A.A∩B＝∅ B.A∪B＝R C.B⊆A D.A⊆B

     

     

    查看答案和解析>>

    同步练习册答案