
已知 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(I)若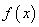 在
在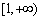 是增函数,求实数
是增函数,求实数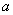 的取值范围;
的取值范围;
(II)当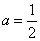 时,求函数
时,求函数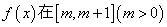 上的最小值;
上的最小值;
(III)求证: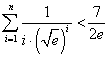 .
.
解:(Ⅰ)由题意知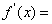
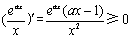 在
在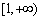 上恒成立.
上恒成立.
又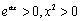 ,则
,则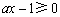 在
在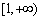 上恒成立,
上恒成立,
即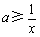 在
在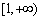 上恒成立. 而当
上恒成立. 而当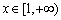 时,
时,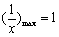 ,所以
,所以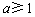 ,
,
于是实数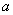 的取值范围是
的取值范围是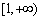 . ………………………………4分
. ………………………………4分
(Ⅱ)当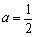 时,则
时,则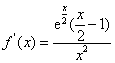 .
.
当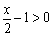 ,即
,即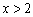 时,
时,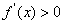 ;
;
当 ,即
,即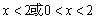 时,
时,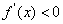 .
.
则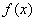 的增区间为(2,+∞),减区间为(-∞,0),(0,2). ……6分
的增区间为(2,+∞),减区间为(-∞,0),(0,2). ……6分
因为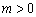 ,所以
,所以 ,
,
①当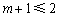 ,即
,即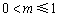 时,
时,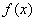 在[
在[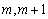 ]上单调递减,
]上单调递减,
所以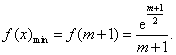
②当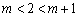 ,即
,即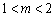 时,
时,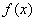 在
在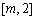 上单调递减,
上单调递减,
在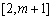 上单调递增,所以
上单调递增,所以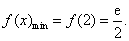
③当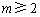 时,
时,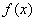 在[
在[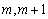 ]上单调递增,所以
]上单调递增,所以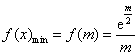 .
.
综上,当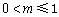 时,
时,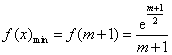 ;
;
当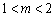 时,
时,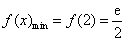 ;
;
当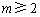 时,
时,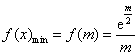 . …………………………9分
. …………………………9分
(Ⅲ)由(Ⅱ)可知,当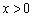 时,
时,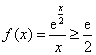 ,所以
,所以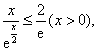
可得 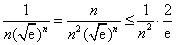 ………………………………11分
………………………………11分
于是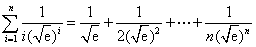
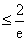
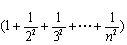
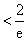
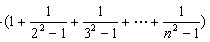
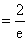
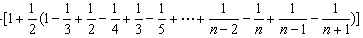
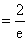
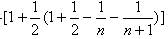
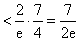 ……………………………………14分
……………………………………14分
【思路点拨】(Ⅰ)由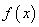 是增函数,转化为
是增函数,转化为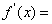
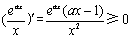 在
在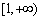 上恒成立. 即
上恒成立. 即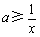 在
在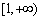 上恒成立. 最后得实数
上恒成立. 最后得实数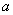 的取值范围(II)当
的取值范围(II)当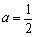 时,求出
时,求出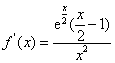 .利用
.利用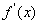 在求出单调区间,然后用分类讨论的思想方法解得
在求出单调区间,然后用分类讨论的思想方法解得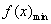
(III)由(Ⅱ)可知,当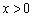 时,
时,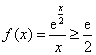 ,所以
,所以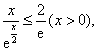
可得 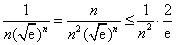 ,然后利用放缩法证明不等式即可.
,然后利用放缩法证明不等式即可.


科目:高中数学 来源: 题型:
某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有 .
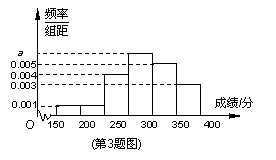 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆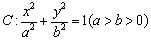 的左、右焦点分别为
的左、右焦点分别为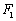 、
、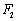 ,过
,过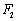 作直线
作直线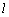 与椭圆
与椭圆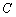 交于点
交于点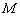 、
、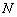 .
.
(1)若椭圆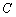 的离心率为
的离心率为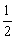 ,右准线的方程为
,右准线的方程为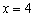 ,
,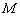 为椭圆
为椭圆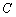 上顶点,直线
上顶点,直线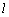 交右准线于点
交右准线于点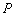 ,求
,求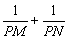 的
的 值;
值;
(2)当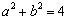 时,设
时,设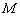 为椭圆
为椭圆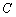 上第一象限内的点,直线
上第一象限内的点,直线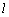 交
交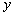 轴于点
轴于点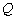 ,
,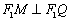 ,证明:点
,证明:点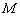 在定直线上.
在定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com