
已知数列{an}满足a1+a2+…+an=n2(n∈N*).
(1) 求数列{an}的通项公式;
(2) 对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使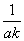 ,
,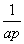 ,
,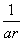 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
解:(1) 当n=1时,a1=1;当n≥2,n∈N*时,a1+a2+…+an-1=(n-1)2,所以an=n2-(n-1)2=2n-1;综上所述,an=2n-1(n∈N*).
(2) 当k=1时,若存在p,r使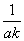 ,
,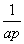 ,
,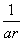 成等差数列,则
成等差数列,则 .因为p≥2,所以ar<0与数列{an}为正数相矛盾,因此,当k=1时不存在;
.因为p≥2,所以ar<0与数列{an}为正数相矛盾,因此,当k=1时不存在;
当k≥2时,设ak=x,ap=y,ar=z,则 ,所以z=
,所以z= .令y=2x-1,得z=xy=x(2x-1),此时ak=x=2k-1,ap=y=2x-1=2(2k-1)-1,所以p=2k-1,ar=z=(2k-1)(4k-3)=2(4k2-5k+2)-1,所以r=4k2-5k+2.
.令y=2x-1,得z=xy=x(2x-1),此时ak=x=2k-1,ap=y=2x-1=2(2k-1)-1,所以p=2k-1,ar=z=(2k-1)(4k-3)=2(4k2-5k+2)-1,所以r=4k2-5k+2.
综上所述,当k=1时,不存在p,r;当k≥2时,存在p=2k-1,r=4k2-5k+2满足题设.


科目:高中数学 来源: 题型:
已知数列{an}的前n项和为Sn,a1=1,且2an+1=Sn+2(n∈N).
(1) 求a2,a3的值,并求数列{an}的通项公式;
(2) 解不等式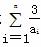 >Sn(n∈N).
>Sn(n∈N).
查看答案和解析>>
科目:高中数学 来源: 题型:
某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1) 求该企业使用该设备x年的年平均污水处理费用y(万元);
(2) 为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
查看答案和解析>>
科目:高中数学 来源: 题型:
设1=a1≤a2≤…≤a7,其中a1,a3,a5,a7成公比为q的等
比数列,a2,a4,a6成公差为1的等差数列,则q的最小值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,a、b、c分别表示三个内角∠A、∠B、∠C的对边,如果(a2+b2)sin(A-B)=(a2-b2)sin(A+B),判断三角形的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
要测量河对岸A、B两点之间的距离,选取相距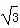 km的C、D两点,并且测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.
km的C、D两点,并且测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com