某化工企业2007年底投入100万元，购入一套污水处理设备．该设备每年的运转费用是0.5万元，此外每年都要花费一定的维护费，第一年的维护费为2万元，由于设备老化，以后每年的维护费都比上一年增加2万元．
(1) 求该企业使用该设备x年的年平均污水处理费用y(万元)；
(2) 为使该企业的年平均污水处理费用最低，该企业几年后需要重新更换新的污水处理设备？
科学实验活动册系列答案科目：高中数学 来源： 题型：
若数列{an}满足an＋1＝an＋an＋2(n∈N*)，则称数列{an}为“凸数列”．
(1) 设数列{an}为“凸数列”，若a1＝1，a2＝－2，试写出该数列的前6项，并求出前6项之和；
(2) 在“凸数列”{an}中，求证：an＋3＝－an，n∈N*；
(3) 设a1＝a，a2＝b，若数列{an}为“凸数列”，求数列前2011项和S2 011.
查看答案和解析>>
科目：高中数学 来源： 题型：
已知数列{an}的前n项和为Sn＝3n－1.
(1) 求数列{an}的通项公式；
(2) 若bn＝log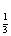
(Sn＋1)，求数列{bnan}的前n项和Tn.
查看答案和解析>>
科目：高中数学 来源： 题型：
已知数列{an}的前n项和为Sn，对一切正整数n，点Pn(n，Sn)都在函数f(x)＝x2＋2x的图象上，且在点Pn(n，Sn)处的切线的斜率为kn.
(1) 求数列{an}的通项公式；
(2) 若bn＝2knan，求数列{bn}的前n项和Tn.
查看答案和解析>>
科目：高中数学 来源： 题型：
已知等差数列{an}满足：an＋1>an(n∈N*)，a1＝1，该数列的前三项分别加上1，1，3后顺次成为等比数列{bn}的前三项．
(1) 分别求数列{an}、{bn}的通项公式；
(2) 设Tn＝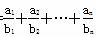
(n∈N*)，若Tn＋
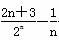<c(c∈Z)恒成立，求c的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知数列{an}满足a1＋a2＋…＋an＝n2(n∈N*)．
(1) 求数列{an}的通项公式；
(2) 对任意给定的k∈N*，是否存在p，r∈N*(k<p<r)使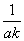
，
，
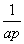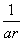成等差数列？若存在，用k分别表示p和r(只要写出一组)；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
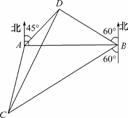
如图，A、B是海面上位于东西方向相距5(3＋
)海里的两个观测点，现位于A点北偏东45°、B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距20海里的C点的救援船立即前往营救，其航行速度为30海里/小时，该救援船达到D点需要多长时间？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
＋1.5(x＞0)．
＋1.5＝21.5，
