
已知数列{an}的前n项和为Sn=3n-1.
(1) 求数列{an}的通项公式;
(2) 若bn=log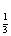 (Sn+1),求数列{bnan}的前n项和Tn.
(Sn+1),求数列{bnan}的前n项和Tn.
解:(1) 当n=1时,a1=S1=2,
当n≥2时,an=Sn-Sn-1=(3n-1)-(3n-1-1)=2×3n-1,
综上所述,an=2×3n-1.
(2) bn=log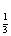 (Sn+1)=log
(Sn+1)=log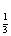 3n=-n,
3n=-n,
所以bnan=-2n×3n-1,
Tn=-2×1-4×31-6×32-…-2n×3n-1,
3Tn=-2×31-4×32-…-2(n-1)×3n-1-2n×3n,
相减,得
-2Tn=-2×1-2×31-2×32-…-2×3n-1+2n×3n
=-2×(1+31+32+…+3n-1)+2n×3n,
所以Tn=(1+31+32+…+3n-1)-n×3n=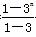 -n×3n
-n×3n
=-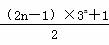 ,n∈N*.
,n∈N*.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
已知数列{an}的前n项和为Sn,a1=1,且2an+1=Sn+2(n∈N).
(1) 求a2,a3的值,并求数列{an}的通项公式;
(2) 解不等式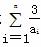 >Sn(n∈N).
>Sn(n∈N).
查看答案和解析>>
科目:高中数学 来源: 题型:
某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1) 求该企业使用该设备x年的年平均污水处理费用y(万元);
(2) 为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
查看答案和解析>>
科目:高中数学 来源: 题型:
设1=a1≤a2≤…≤a7,其中a1,a3,a5,a7成公比为q的等
比数列,a2,a4,a6成公差为1的等差数列,则q的最小值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
要测量河对岸A、B两点之间的距离,选取相距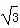 km的C、D两点,并且测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.
km的C、D两点,并且测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com