练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     已知数列an＝求a1＋a2＋a3＋a4＋…＋a99＋a100的值．


    解：由题意得a1＋a2＋a3＋a4＋…＋a99＋a100＝0＋2＋2＋4＋4＋…＋98＋98＋100＝2(2＋4＋6＋…＋98)＋100＝2×＋100＝5 000.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     已知a1＝1，an＝n(an＋1－an)(n∈N*)，则数列{an}的通项公式是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在(－∞，0)∪(0，＋∞)上的函数f(x)，如果对于任意给定的等比数列{an}，{f(an)}仍是等比数列，则称f(x)为“保等比数列函数”．现有定义在(－∞，0)∪(0，＋∞)上的如下函数：

    ①f(x)＝x2；②f(x)＝2x；③f(x)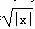＝；④f(x)＝ln(x)．

    其中是“保等比数列函数”的是__________．(填序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    求下面数列的前n项和：

    1，3，5，7， …

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn＝3n－1.

    (1) 求数列{an}的通项公式；

    (2) 若bn＝log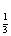(Sn＋1)，求数列{bnan}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某种细胞开始时有2个，1小时后分裂成4个并死去1个，2小时后分裂成6个并死去1个，3小时后分裂成10个并死去1个，…，按照此规律，6小时后，细胞的存活数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等差数列{an}满足：an＋1>an(n∈N*)，a1＝1，该数列的前三项分别加上1，1，3后顺次成为等比数列{bn}的前三项．

    (1) 分别求数列{an}、{bn}的通项公式；

    (2) 设Tn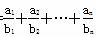＝ (n∈N*)，若Tn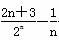＋<c(c∈Z)恒成立，求c的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}中，a1＝2，n∈N*，an＞0，数列{an}的前n项和为Sn，且满足an＋1＝.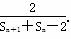

    (1) 求{Sn}的通项公式；

    (2) 设{bk}是{Sn}中的按从小到大顺序组成的整数数列．

    ① 求b3；

    ② 存在N(N∈N*)，当n≤N时，使得在{Sn}中，数列{bk}有且只有20项，求N的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


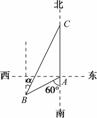
    如图，渔船甲位于岛屿A的南偏西60°方向的B处，且与岛屿A相距12海里，渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行，若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙，刚好用2 h追上，此时到达C处．

    (1) 求渔船甲的速度；

    (2) 求sinα的值．

    查看答案和解析>>

    同步练习册答案