
已知数列{an}中,a1=2,n∈N*,an>0,数列{an}的前n项和为Sn,且满足an+1=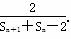 .
.
(1) 求{Sn}的通项公式;
(2) 设{bk}是{Sn}中的按从小到大顺序组成的整数数列.
① 求b3;
② 存在N(N∈N*),当n≤N时,使得在{Sn}中,数列{bk}有且只有20项,求N的范围.
解:(1) an+1=Sn+1-Sn,
∴ (Sn+1-Sn)(Sn+1+Sn-2)=2;
即(Sn+1)2-(Sn)2-2(Sn+1-Sn)=2,
∴ (Sn+1-1)2-(Sn-1)2=2,且(S1-1)2=1,
∴ {(Sn-1)2}是首项为1,公差为2的等差数列,
∴ Sn=1+ .
.
(2) ① n=1时,S1=1+1=2=b1,n=5时,S5=1+3=4=b2,n=13时,S13=1+5=6=b3.
② ∵ 2n-1是奇数,Sn=1+ 为有理数,则
为有理数,则 =2k-1,
=2k-1,
∴ n=2k2-2k+1,
当k=20时,n=761;当k=21时,n=841;
∴ 存在N∈[761,840],当n≤N时,使得在{Sn}中,数列{bk}有且只有20项.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
已知数列{an}前n项和为Sn,且a2an=S2+Sn对一切正整数都成立.
(1) 求a1,a2的值;
(2) 设a1>0,数列 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设1=a1≤a2≤…≤a7,其中a1,a3,a5,a7成公比为q的等
比数列,a2,a4,a6成公差为1的等差数列,则q的最小值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.
(1) 若c=2,C=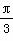 ,且△ABC的面积为
,且△ABC的面积为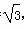 ,求a、b的值;
,求a、b的值;
(2) 若sinC+sin(B-A)=sin2A,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,角A、B、C对应的边分别是a、b、c.已知cos2A-3cos(B+C)=1.
(1) 求角A的大小;
(2) 若△ABC的面积S=5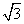 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com