
分析 (1)由正弦定理,三角函数恒等变换的应用化简已知可得$\sqrt{3}sinCsinA+cosAsinC-2sinC=0$,结合sinC≠0,可得$sin(A+\frac{π}{6})=1$,结合A的范围可求A的值.
(2)由三角形内角和定理,三角函数恒等变换的应用可求cosB+cosC=sin(C+$\frac{π}{6}$),结合范围$\frac{π}{6}<C<\frac{π}{2}$,利用正弦函数的性质可求范围.
解答 解:(1)因为$\sqrt{3}csinA-acosC+b-2c=0$,
所以$\sqrt{3}sinCsinA-sinAcosC+sinB-2sinC=0$,
因为sinB=sin(A+C)=sinAcosC+cosAsinC,
所以$\sqrt{3}sinCsinA+cosAsinC-2sinC=0$,
又sinC≠0,
所以$\sqrt{3}sinA+cosA=2$,可得:$sin(A+\frac{π}{6})=1$,
因为△ABC是锐角三角形,
所以,$A+\frac{π}{6}=\frac{π}{2}$,$A=\frac{π}{3}$,
(2)因为$A=\frac{π}{3}$,
所以$B+C=\frac{2π}{3}$,$cosB+cosC=cos({\frac{2π}{3}-C})+cosC=sin({C+\frac{π}{6}})$,
因为△ABC是锐角三角形,
所以$\frac{π}{6}<C<\frac{π}{2}$,cosB+cosC的范围$({\frac{{\sqrt{3}}}{2},1})$.
点评 本题主要考查了正弦定理,三角函数恒等变换的应用,三角形内角和定理,正弦函数的性质在解三角形中的应用,考查了转化思想和数形结合思想,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 男生 | 15 | 35 | 50 |
| 女生 | 30 | 40 | 70 |
| 总计 | 45 | 75 | 120 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | ||
| 合计 | 70 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
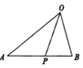 如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )| A. | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B. | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C. | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D. | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com