练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．复数z=$\frac{1}{1+i}$（i是虚数单位）的共轭复数在复平面上对应的点位于第（　　）象限．
    A．一B．二C．三D．四

    分析 利用复数的运算法则、共轭复数的定义、几何意义即可得出．

    解答 解：z=$\frac{1}{1+i}$=$\frac{1-i}{（1+i）（1-i）}$=$\frac{1}{2}-\frac{1}{2}i$的共轭复数为$\frac{1}{2}+\frac{1}{2}i$在复平面上对应的点$（\frac{1}{2}，\frac{1}{2}）$位于第一象限．
    故选：A．

    点评 本题考查了复数的运算法则、共轭复数的定义、几何意义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．已知△ABC的重心为O，且AB=5，BC=2$\sqrt{3}$，AC=3，则$\overrightarrow{AO}$•$\overrightarrow{BC}$=-$\frac{16}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=xlnx-3x+8．
    （1）求函数y=f（x）在[e，e3]（e是自然对数的底数）的值域；
    （2）设0＜a＜b，求证：$0＜2f（a）+f（b）-3f（{\frac{2a+b}{3}}）＜（{b-a}）ln3$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．半径为1的球的表面积为（　　）
    A．πB．$\frac{4}{3}π$C．2πD．4π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

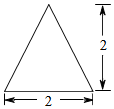    10．一个四棱锥的侧棱长都相等，底面是正方形，其正（主）视图如图所示，则该四棱锥的侧面积是（　　）
    A．$4\sqrt{3}$B．$4\sqrt{5}$C．$4（{\sqrt{5}+1}）$D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

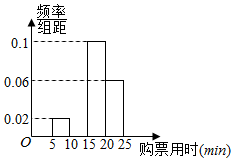    20．某车站在春运期间为了了解旅客购票情况，随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t（以下简称为购票用时，单位为min），下面是这次调查统计分析得到的频率分布表和频率分布直方图（如图所示）．
    分组组距频数频率
    一组0≤t＜500
    二组5≤t＜10100.10
    三组10≤t＜1510②
    四组15≤t＜20①0.50
    五组20≤t≤25300.30
    合计0≤t≤251001.00
    解答下列问题：
    （1）这次抽样的样本容量是多少？
    （2）在表中填写出缺失的数据并补全频率分布直方图；
    （3）旅客购票用时的中位数为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．如果命题P：点（1，-1）在曲线y=-1+lnx上；命题q：$\int_0^{\frac{π}{2}}{sinxdx}$计算结果是-1，那么命题p∧q的真假性为假 （写真或假）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．某中学在运动会期间举行定点投篮比赛，规定每人投篮3次，投中一球得1分，没有投中得0分，假设每次投篮投中与否是相互独立的．已知小明每次投篮投中的概率都是$\frac{1}{3}$．
    （1）求小明在投篮过程中直到第三次才投中的概率；
    （2）求小明在3次投篮后的总得分ξ的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

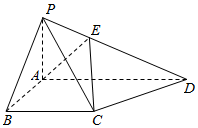    5．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，∠ABC=∠BAD=90°，且PA=AB=BC=$\frac{1}{2}$AD=1，PA⊥平面ABCD．
    （1）求PB与平面PCD所成角的正弦值；
    （2）棱PD上是否存在一点E满足∠AEC=90°？

    查看答案和解析>>

    同步练习册答案