
| 赔付金额(元) | 0 | 1000 | 2000 | 3000 | 4000 |
| 车辆数 | 500 | 150 | 200 | 100 | 50 |
分析 (1)设A表示事件“赔付金额为3000元,”B表示事件“赔付金额为4000元”,以频率估计概率,求得P(A),P(B),再根据投保额为2800元,赔付金额大于投保金额得情形是3000元和4000元,问题得以解决.
(2)先计算从新司机中任取两人的方法总数,及这两人的赔付金额之和不小于投保金额之和方法个数,代入古典概型概率计算公式,可得答案.
解答 解:(1)设A表示事件“赔付金额为3000元,”B表示事件“赔付金额为4000元”,以频率估计概率得
P(A)=$\frac{100}{500+150+200+100+50}$=0.1,
P(B)=$\frac{50}{500+150+200+100+50}$=0.05,
由于投保额为2800元,赔付金额大于投保金额得情形是3000元和4000元,所以其概率为P(A)+P(B)=0.1+0.05=0.15.
(2)由已知,样本车辆中车主为新司机的有1%×200+2%×100+4%×50=6人,
计赔付金额为2000元、3000元和4000元的分别为:A,B,C,D,E,F,
则从新司机中任取两人共有${C}_{6}^{2}$=15种不同的取法,分别为:
AB,AC,AD,AE,AF,
BC,BD,BD,BF,CD,
CE,CF,DE,DF,EF,
其中这两人的赔付金额之和不小于投保金额之和的事件有:
CD,CE,CF,DE,DF,EF,共6种,
故这两人的赔付金额之和不小于投保金额之和的概率P=$\frac{6}{15}$=$\frac{2}{5}$
点评 本题主要考查了用频率来表示概率,古典概率的概率计算公式,难度不大,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 先把各点的横坐标缩短到原来的$\frac{1}{2}$倍,再向右平移$\frac{5π}{12}$个单位 | |
| B. | 先把各点的横坐标伸长到原来的2倍,再向右平移$\frac{5π}{6}$个单位 | |
| C. | 先把各点的横坐标缩短到原来的$\frac{1}{2}$倍,再向左平移$\frac{5π}{12}$个单位 | |
| D. | 先把各点的横坐标伸长到原来的2倍,再向左平移$\frac{5π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1km.求B,D的距离$\frac{{3\sqrt{2}+\sqrt{6}}}{20}$.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1km.求B,D的距离$\frac{{3\sqrt{2}+\sqrt{6}}}{20}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
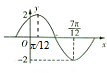 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图,求:
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com