
分析 用换元法求得(1)和(2)中的函数的解析式;用待定系数法求得(3)中的函数解析式;用解方程组的方法,求出(4)中的函数的解析式.
解答 解:(1)∵已知f(x+1)=x2 ,令x+1=t,可得x=t-1,∴f(t)=(t-1)2,∴f(x)=(x-1)2.
(2)∵已知f($\frac{1-x}{1+x}$)=x,令 $\frac{1-x}{1+x}$=t,求得 x=$\frac{1-t}{1+t}$,∴f(t)=$\frac{1-t}{1+t}$,∴f(x)=$\frac{1-x}{1+x}$.
(3)已知函数f(x)为一次函数,设f(x)=kx+b,k≠0,
∵f[f(x)]=kf(x)+b=k(kx+b)+b=9x+1,∴k=3,b=$\frac{1}{4}$,或k=-3,b=-$\frac{1}{2}$,求
∴f(x)=3x+$\frac{1}{4}$,或f(x)=-3x-$\frac{1}{2}$.
(4)∵已知3f(x)-f($\frac{1}{x}$)=x2 ①,∴用$\frac{1}{x}$代替x,可得3f($\frac{1}{x}$)-f(x)=$\frac{1}{{x}^{2}}$ ②,
由①②求得f(x)=$\frac{3}{8}$x2+$\frac{1}{{8x}^{2}}$.
点评 本题主要考查求函数的解析式常用的几种方法,属于中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 48 | C. | 42 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
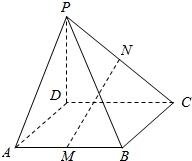 如图.在四棱锥P-ABCD中.底面ABCD是平行四边形,点M为棱AB上一点AM=2MB.点N为棱PC上一点,
如图.在四棱锥P-ABCD中.底面ABCD是平行四边形,点M为棱AB上一点AM=2MB.点N为棱PC上一点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2(1-$\frac{1}{{2}^{n}}$) | B. | 2(1+$\frac{1}{{2}^{n}}$) | C. | 2($\frac{1}{{2}^{n}}$-1) | D. | 2($\frac{1}{{2}^{n}}$+1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com