练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．某公共汽车上有10位乘客，沿途5个车站，乘客下车的可能方式有（　　）种．
    A．510B．105C．50D．A105

    分析 根据题意，分析可得每个乘客有5种下车的方式，由分步计数原理计算可得答案．

    解答 解：根据题意，公共汽车沿途5个车站，
    则每个乘客有5种下车的方式，
    则10位乘客共有510种下车的可能方式；
    故选：A．

    点评 本题考查排列、组合的实际应用，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．等差数列{an}满足a12+a2n+12=1，则an+12+a3n+12的取值范围是[2，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知P为圆x2+y2=4上的动点．定点A的坐标为（3，4），则线段AP中点M的轨迹方程（x-$\frac{3}{2}$）2+（y-2）2=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

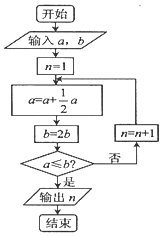    20．宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．如图是源于其思想的一个程序框图，若输入的a，b分别为3，2，则输出的n=（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．使奇函数f（x）=sin（2x+θ）+$\sqrt{3}$cos（2x+θ）在[-$\frac{π}{4}$，0]上为减函数的θ（θ∈（0，π））的值为$\frac{2π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列函数中，既是偶函数又在区间（0，+∞）上单调递减的是（　　）
    A．y=$\frac{1}{x}$B．y=|x|-1C．y=lg xD．y=（$\frac{1}{2}$）|x|

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知集合A={x|lnx≤0}，B={x∈R|z=x+i，$|z|≥\frac{{\sqrt{5}}}{2}$，i是虚数单位}，A∩B=（　　）
    A．$（{-∞，-\frac{1}{2}}]∪[{\frac{1}{2}，1}]$B．$[{\frac{1}{2}，1}]$C．（0，1]D．[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知函数f（x）=ex-kx2在区间（0，+∞）上单调递增，则k的取值范围是（-∞，$\frac{e}{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．某化肥厂生产甲、乙两种混合肥料，需要A，B，C三种主要原料，生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示：
    肥料  原料ABC
    甲483
    乙5510
    现有A种原料200吨，B种原料360吨，C种原料300吨，在此基础上生产甲、乙两种肥料．已知生产1车皮甲种肥料，产生的利润为2万元；生产1车皮乙种肥料，产生的利润为3万元、分别用x，y表示计划生产甲、乙两种肥料的车皮数．
    （Ⅰ）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
    （Ⅱ）问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润．

    查看答案和解析>>

    同步练习册答案