
| ���� ԭ�� | A | B | C |
| �� | 4 | 8 | 3 |
| �� | 5 | 5 | 10 |
���� ���������������������ʽ��ϵ����������������
�������Ŀ�꺯��������ƽ��ֱ�߷�������⼴�ɣ�
���  �⣺��������֪x��y���㲻��ʽ$\left\{\begin{array}{l}{4x+5y��200}\\{8x+5y��360}\\{3x+10y��300}\\{x��0��y��0}\end{array}\right.$����ʽ��Ӧ��ƽ������Ϊ��
�⣺��������֪x��y���㲻��ʽ$\left\{\begin{array}{l}{4x+5y��200}\\{8x+5y��360}\\{3x+10y��300}\\{x��0��y��0}\end{array}\right.$����ʽ��Ӧ��ƽ������Ϊ��
������������Ϊz��Ԫ����Ŀ�꺯��Ϊz=2x+3y����y=-$\frac{2}{3}$x+$\frac{z}{3}$��
ƽ��ֱ��y=-$\frac{2}{3}$x+$\frac{z}{3}$����ͼ��õ�ֱ�߾�����Mʱ��ֱ�ߵĽؾ����ʱz���
��$\left\{\begin{array}{l}{4x+5y=200}\\{3x+10y=300}\end{array}\right.$��$\left\{\begin{array}{l}{x=20}\\{y=24}\end{array}\right.$����M��20��24����
��ʱz=40+72=112��
���ֱ���������20��Ƥ���ҷ���24��Ƥ���ܹ��������������������Ϊ112��Ԫ��
���� ������Ҫ�������Թ滮��Ӧ�ã�������������Լ����������������������ƽ�Ʒ��ǽ������Ĺؼ���


 ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 510 | B�� | 105 | C�� | 50 | D�� | A105 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 2 | C�� | 3 | D�� | -3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{23}{9}$ | B�� | -$\frac{20}{31}$ | C�� | -6 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
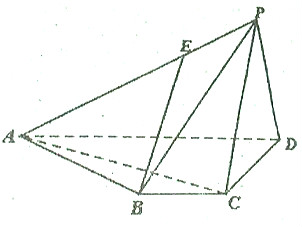 ��ͼ������P-ABCD�У�BC��AD��BC=1��AD=3��AC��CD����ƽ��PCD��ƽ��ABCD��
��ͼ������P-ABCD�У�BC��AD��BC=1��AD=3��AC��CD����ƽ��PCD��ƽ��ABCD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com