
【题目】如图1,在边长为1的等边三角形![]() 中,
中,![]() 分别是
分别是![]() 边上的点,
边上的点,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥![]() ,其中
,其中![]() .
.
(1) 证明:![]() //平面
//平面![]() ;
;
(2) 证明:![]()
![]() 平面
平面![]() ;
;
(3) 当![]() 时,求三棱锥
时,求三棱锥![]() 的体积
的体积![]() .
.

【答案】(1)详见解析;(2)详见解析;(3)![]() 。
。
【解析】
试题分析:(1)因为三角形ABC为等边三角形,所以AB=AC,又AD=AE,所以![]() ,则DE//BC,折叠后图1中,DG//BF,GE//CF,又因为
,则DE//BC,折叠后图1中,DG//BF,GE//CF,又因为![]() ,
,![]() ,根据面面平行的判断定理可知,平面DGE//平面BCF,DE
,根据面面平行的判断定理可知,平面DGE//平面BCF,DE![]() 平面DGE,所以DE//平面BFC;(2)图1中,F为BC中点,所以BC⊥AF,BF=FC=
平面DGE,所以DE//平面BFC;(2)图1中,F为BC中点,所以BC⊥AF,BF=FC=![]() ,又因为BC=
,又因为BC=![]() ,所以BF2+FC2=BC2,则CF⊥BF,因为AF
,所以BF2+FC2=BC2,则CF⊥BF,因为AF![]() BF=F,根据线面垂直判定定理,所以CF⊥平面ABF;(3)由图4可知,AF⊥DE,所以图1中,AG⊥DG,AG⊥GE,且DG
BF=F,根据线面垂直判定定理,所以CF⊥平面ABF;(3)由图4可知,AF⊥DE,所以图1中,AG⊥DG,AG⊥GE,且DG![]() GE=G,所以AG⊥平面DGE,所以F到平面DGE的距离等于线段GF的长,又因为AD=
GE=G,所以AG⊥平面DGE,所以F到平面DGE的距离等于线段GF的长,又因为AD=![]() ,所以
,所以![]() ,则DE=
,则DE=![]() ,
,![]() ,所以GF=
,所以GF=![]() AF,又因为AF=
AF,又因为AF=![]() ,所以GF=
,所以GF=![]() ,因为DE//BC,所以G为DE中点,DG=GE=
,因为DE//BC,所以G为DE中点,DG=GE=![]() DE=
DE=![]() ,又因为DE//BF,GE//CF,所以DG⊥GE,所以三角形DGE的面积为
,又因为DE//BF,GE//CF,所以DG⊥GE,所以三角形DGE的面积为![]() ,三棱锥F-DGE的体积为
,三棱锥F-DGE的体积为![]() 。
。
试题解析:(1)![]() ,在折叠后的三棱锥
,在折叠后的三棱锥![]() 中
中
也成立,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)在等边三角形![]() 中,
中,![]() 是
是![]() 的中点,所以
的中点,所以![]() ①,
①,![]() .
.
![]() 在三棱锥
在三棱锥![]() 中,
中,![]() ,
,![]() ②
②
![]() ;
;
(3)由(1)可知![]() ,结合(2)可得
,结合(2)可得![]() .
.
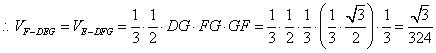


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】全称命题“所有被5整除的整数都是奇数”的否定 ( )
A. 所有被5整除的整数都不是奇数 B. 所有奇数都不能被5整除
C. 存在被5整除的整数不是奇数 D. 存在奇数,不能被5整除
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>2)=0.023,
则P(-2≤ξ≤2)=( )
A. 0.477 B. 0.628 C. 0.954 D. 0.977
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间![]() 上的函数
上的函数![]() ,若存在闭区间
,若存在闭区间![]() 和常数
和常数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且对任意
,且对任意![]() ,当
,当![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 为区间
为区间![]() 上的“平底型”函数.
上的“平底型”函数.
(1)判断函数![]() 和
和![]() 是否为
是否为![]() 上的“平底型”函数?
上的“平底型”函数?
(2)若函数![]() 是区间
是区间![]() 上的“平底型”函数,求
上的“平底型”函数,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】文科做:数列![]() 中,
中,![]() 且满足
且满足![]()
![]()
(I)求数列![]() 的通项公式;
的通项公式;
(II)设![]() ,求
,求![]() ;
;
(III)设![]() =
=![]()
![]() ,是否存在最大的整数
,是否存在最大的整数![]() ,使得对任意
,使得对任意![]() ,均有
,均有![]()
![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: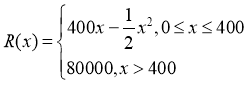 ,其中
,其中![]() 是仪器的月产量.
是仪器的月产量.
(1) 将利润表示为月产量的函数![]() ;
;
(2) 当月产量为何值时,公司所获利润最大?最大利润为多少元? (利润=总收益-总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 是等边三角形.已知
是等边三角形.已知![]() ,
,![]() ,
,![]() .
.

(1)设![]() 是
是![]() 上的一点,证明:平面
上的一点,证明:平面![]() 平面
平面![]() ;
;
(2)当![]() 点位于线段
点位于线段![]() 什么位置时,
什么位置时,![]() 平面
平面![]() ?
?
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂用7万元钱购买了一台新机器,运输安装费用2千元,每年投保、动力消耗的费用也为2千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,依此类推,即每年增加1千元.问这台机器最佳使用年限是多少年?并求出年平均费用的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com