
| A. | {x|x>-2012} | B. | {x|x<-2012} | C. | {x|-2012<x<0} | D. | {x|-2017<x<-2012} |
分析 构造函数g(x)=x2f(x),x>0,求出函数的单调性,问题转化为g(x-2015)>g(2),从而求出不等式的解集即可.
解答 解:令g(x)=x2f(x),x>0,
则g′(x)=x[2f(x)+xf′(x)]>0,
∴g(x)在(0,+∞)递增,
∵不等式$\frac{{({x+2017})f({x+2017})}}{5}$$<\frac{5f(5)}{x+2017}$,可得(x+2017)2f(x+2017)<25f(5),
∴g(x+2017)<g(5),
∴0<x+2017<5,解得:-2017<x<-2012,
则不等式$\frac{{({x+2017})f({x+2017})}}{5}$$<\frac{5f(5)}{x+2017}$的解集为:{x|-2017<x<-2012}.
故选:D.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | q=$\frac{1}{4}$ | B. | q=-$\frac{1}{4}$ | C. | q=4 | D. | q=-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
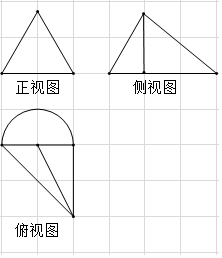
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
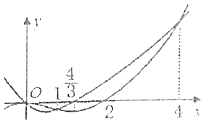 已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )
已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )| A. | (0,4) | B. | $({-∞,1}),({\frac{4}{3},4})$ | C. | (0,1),(4,+∞) | D. | (-∞,0),(1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com