
分析 直接利用导数的定义求函数f(x)=$\sqrt{{x^2}+1}$在x=1处的导数值.
解答 解:△y=f(1+△x)-f(1)=$\sqrt{(1+△x)^{2}+1}$-$\sqrt{2}$=$\sqrt{△{x}^{2}+2△x+2}$-$\sqrt{2}$,
∴$\frac{△y}{△x}$=$\frac{\sqrt{△{x}^{2}+2△x+2}-\sqrt{2}}{△x}$,
∴f′(1)=$\underset{lim}{△x→0}$$\frac{\sqrt{△{x}^{2}+2△x+2}-\sqrt{2}}{△x}$=$\underset{lim}{△x→0}$$\frac{△{x}^{2}+2△x}{△x(\sqrt{△{x}^{2}+2△x+2}+\sqrt{2})}$
=$\underset{lim}{△x→0}$$\frac{△x+2}{\sqrt{△{x}^{2}+2△x+2}+\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查的知识点是导数的运算,难度不大,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.3 | C. | 0.4 | D. | 0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
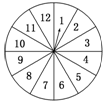 某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如下图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动.
某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如下图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-2012} | B. | {x|x<-2012} | C. | {x|-2012<x<0} | D. | {x|-2017<x<-2012} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com