
分析 (1)利用向量共线直接写出夹角,然后利用向量的数量积求解即可.
(2)利用向量垂直数量积为0,列出方程求解即可.
解答 (10分) 解:(1)∵|$\overrightarrow a$|=1,|$\overrightarrow b$|=$\sqrt{2}$,$\overrightarrow a$∥$\overrightarrow b$,∴θ=0°或180°,
∴$\overrightarrow a$•$\overrightarrow b$=|$\overrightarrow a$||$\overrightarrow b$|cosθ=±$\sqrt{2}$.…5’
(2)∵$\overrightarrow{a}$-$\overrightarrow b$与$\overrightarrow{a}$垂直;∴($\overrightarrow{a}$-$\overrightarrow b$)•$\overrightarrow{a}$=0,
即|$\overrightarrow{a}$|2-$\overrightarrow{a}$•$\overrightarrow b$=1-$\sqrt{2}$cos θ=0,
∴cos θ=$\frac{\sqrt{2}}{2}$.
又0°≤θ≤180°,∴θ=45°.…10’
点评 本题考查平面向量的数量积的应用,考查向量共线与垂直的充要条件的应用,考查计算能力.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:解答题
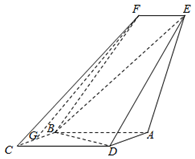 如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=$\sqrt{6}$,DE=3,∠BAD=60°,G为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | q=$\frac{1}{4}$ | B. | q=-$\frac{1}{4}$ | C. | q=4 | D. | q=-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
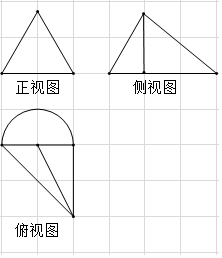
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
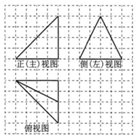 在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )
在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )| A. | 4$\sqrt{3}$ | B. | 6 | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com