练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．若G是△ABC的重心，且满足$\overrightarrow{GA}+\overrightarrow{GB}=λ\overrightarrow{GC}$，则λ=（　　）
    A．1B．-1C．2D．-2

    分析 G是△ABC的重心，可得$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$，利用$\overrightarrow{GA}+\overrightarrow{GB}=λ\overrightarrow{GC}$，即可得出结论．

    解答 解：∵G是△ABC的重心，
    ∴$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$，
    ∵$\overrightarrow{GA}+\overrightarrow{GB}=λ\overrightarrow{GC}$，
    ∴λ=-1，
    故选B．

    点评 本题考查向量知识的运用，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．设l1为曲线f（x）=ex+x（e为自然对数的底数）的切线，直线l2的方程为2x-y+3=0，且l1∥l2，则直线l1与l2的距离为$\frac{2\sqrt{5}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．等比数列{an}的前n项和为Sn，若a2+S3=0，则公比q=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若tanα=3，则${cos^2}（{α+\frac{π}{4}}）-{cos^2}（{α-\frac{π}{4}}）$=（　　）
    A．$-\frac{3}{5}$B．$-\frac{4}{5}$C．$\frac{3}{5}$D．$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知直角△ABC中AB是斜边，$\overrightarrow{CA}$=（3，-9），$\overrightarrow{CB}$=（-3，x），则x的值是（　　）
    A．27B．1C．9D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知函数f（x）=2sinx-3x，若对任意m∈[-2，2]，f（ma-3）+f（a2）＞0的恒成立，则a的取值范围是（　　）
    A．（-1，1）B．（-∞，-1）∪（3，+∞）C．（-3，3）D．（-∞，-3）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．正方体ABCD-A1B1C1D1中，E，F分别是AD，DD1的中点，AB=4，则过B，E，F的平面截该正方体所得的截面周长为（　　）
    A．6$\sqrt{2}$+4$\sqrt{5}$B．6$\sqrt{2}$+2$\sqrt{5}$C．3$\sqrt{2}$+4$\sqrt{5}$D．3$\sqrt{2}$+2$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知数列{an}的前n项和Sn和通项an满足Sn=$\frac{1}{2}$（1-an）．
    （1）求数列{an}的通项公式；
    （2）设函数f（x）=log${\;}_{\frac{1}{3}}$x，bn=f（a1）+f（a2）+…+f（an），Tn=$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{n}}$，求Tn的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

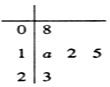    11．如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图，若该运动员在这5场比赛中的得分的中位数为12，则该运动员这5场比赛得分的平均数不可能为（　　）
    A．$\frac{68}{5}$B．$\frac{69}{5}$C．14D．$\frac{71}{5}$

    查看答案和解析>>

    同步练习册答案