
第16届亚运会于2010年11月12日在广州举办,运动会期间来自广州大学和中山大学的共计6名大学生志愿者将被随机平均分配到跳水、篮球、体操这三个比赛场馆服务,且跳水场馆至少有一名广州大学志愿者的概率是 .
.
(1)求6名志愿者中来自广州大学、中山大学的各有几人?
(2)设随机变量X为在体操比赛场馆服务的广州大学志愿者的人数,求X的分布列及均值.
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标3章练习卷(解析版) 题型:填空题
计算下面事件A与事件B的2×2列联表的χ2统计量值,得χ2≈________,从而得出结论________.
| B |
| 总计 |
A | 39 | 157 | 196 |
| 29 | 167 | 196 |
总计 | 68 | 324 | 392 |
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2章练习卷(解析版) 题型:填空题
如图,EFGH是以O为圆心,半径为1的圆内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则(1)P(A)=________;
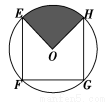
(2)P(B|A)=________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:解答题
甲、乙两名射手各打了10发子弹,其中甲击中环数与次数如下表
环数 | 5 | 6 | 7 | 8 | 9 | 10 |
次数 | 1 | 1 | 1 | 1 | 2 | 4 |
乙射击的概率分布列如表
环数 | 7 | 8 | 9 | 10 |
概率 | 0.2 | 0.3 | p | 0.1 |
(1)若甲,乙两人各打一枪,求共击中18环的概率及p的值;
(2)比较甲,乙两人射击水平的优劣.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:填空题
设一随机试验的结果只有A和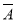 ,且P(A)=p令随机变量X=
,且P(A)=p令随机变量X= ,则X的方差V(X)等于________.
,则X的方差V(X)等于________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:填空题
投掷两个骰子,至少有一个4点或5点出现时,就说这次试验成功,则在10次试验中,成功次数X的期望是________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.4练习卷(解析版) 题型:选择题
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类.这三类工程所含项目的个数分别占总数的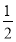 、
、 、
、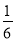 ,现在3名工人独立地从中任选一个项目参与建设.
,现在3名工人独立地从中任选一个项目参与建设.
(1)求他们选择的项目所属类别互不相同的概率;
(2)记X为3人中选择的项目属于基础设施工程或产业建设工程的人数,求X的分布列.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.3练习卷(解析版) 题型:填空题
甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8,0.6,0.5,则三人都达标的概率为________,三人中至少有一人达标的概率为________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1章练习卷(解析版) 题型:解答题
设an=1+q+q2+…+qn-1(n∈N,q≠±1),An=C n1a1+C n2a2+…+Cnnan,求An(用n和q表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com