练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．下列不等式一定成立的是（　　）
    A．lg（x2+$\frac{1}{4}$）＞lgx（x＞0）B．x2+1≥2|x|（x∈R）
    C．sin x+$\frac{1}{sinx}$≥2（x≠kπ，k∈Z）D．$\frac{1}{{x}^{2}+1}$＞1（x∈R）

    分析 A、B  考查了重要不等式a2+b2≥2|ab|，B均值不等式解题必须满足三个基本条件：“一正，二定、三相等”，简单值域求解．

    解答 解：对于A：lg（x2+$\frac{1}{4}$）≥lgx，没有取等号，故A错；对于C：当sinx＞0时，sin x+$\frac{1}{sinx}$≥2 才成立，故C错；对于D  $\frac{1}{{x}^{2}+1}≤1$，故D错．故答案为B．

    点评 本题考查均值不等式解题 的三个基本条件，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．设数列{an}的前n项和Sn满足Sn=2an-a1且a1，a2+1，a3成等差数列．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设数列{nan}的前n项和为Tn，求Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知命题$p：?{x_0}∈R，{2^{{x_0}-1}}≤1$，则命题?p为（　　）
    A．$?{x_0}∈R，{2^{{x_0}-1}}≥1$B．$?{x_0}∈R，{2^{{x_0}-1}}＞1$
    C．?x∈R，2x-1≤1D．?x∈R，2x-1＞1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若函数y=x2lga+2x+4lga有最小值-3，则a=a=10${\;}^{\frac{1}{4}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

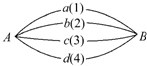    19．如图，从A地到B地设置了4条不同的网络线路，它们通过的最大信息量分别为1，2，3，4，现从中任取三条网线连通A，B两地（三条网线可通过的信息总量即三条网线各自的最大信息量之和）．
    （1）设三条网线可通过的最大信息总量为x，已知当x≥7时，可保证线路信息畅通，求线路信息畅通的概率．
    （2）为保证网络在x≥7时信息畅通的概率超过0.85，需要增加一条最大信息量为n（n≥3，n∈N）的网线与原有4条线路并联，问满足条件的n的最小值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知等差数列{an}中，a3+a8=12，则S10=60．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．$|{\overrightarrow a}|=2，|{\overrightarrow b}|=3，\overrightarrow a与\overrightarrow b的夹角为{60}^0，则|{2\overrightarrow a+\overrightarrow b}$|=$\sqrt{37}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知sin（$\frac{π}{2}$+α）=$\frac{3}{5}$，α∈（0，$\frac{π}{2}$），则sin（π+α）=-$\frac{4}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数f（x）=ax+bx+c（a＞0，a≠1，b，c∈R）
    （1）若b=0，且满足f（2）=1，f（4）=73，求函数f（x）的解析式；
    （2）当a=2时，若对任意x1，x2∈[-1，1]，恒有|f（x1）-f（x2）|≤4，求非负实数b的取值范围．

    查看答案和解析>>

    同步练习册答案