
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | -2 |
分析 由条件求得tan(θ-$\frac{π}{4}$)<-1,利用同角三角函数的基本关系求得sin2θ=cos($\frac{π}{2}$-2θ)的值,再利用二倍角的余弦公式求得tan(θ-$\frac{π}{4}$)的值.
解答 解:∵θ∈($\frac{π}{2}$,π),sinθ+cosθ=-$\frac{{\sqrt{10}}}{5}$,∴θ∈($\frac{3π}{4}$,π),∴θ-$\frac{π}{4}$∈($\frac{π}{2}$,$\frac{3π}{4}$),tan(θ-$\frac{π}{4}$)<-1.
故1+2sinθcosθ=$\frac{2}{5}$,∴sin2θ=cos($\frac{π}{2}$-2θ)=$\frac{{cos}^{2}(\frac{π}{4}-θ){-sin}^{2}(\frac{π}{4}-θ)}{{cos}^{2}(\frac{π}{4}-θ){+sin}^{2}(\frac{π}{4}-θ)}$=$\frac{1{-tan}^{2}(\frac{π}{4}-θ)}{1{+tan}^{2}(\frac{π}{4}-θ)}$=-$\frac{3}{5}$,
求得tan(θ-$\frac{π}{4}$)=±2,故tan(θ-$\frac{π}{4}$)=-2,
故选:D.
点评 本题主要考查同角三角函数的基本关系、二倍角的余弦公式的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
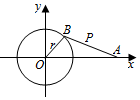 如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.
如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{5}{9}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com